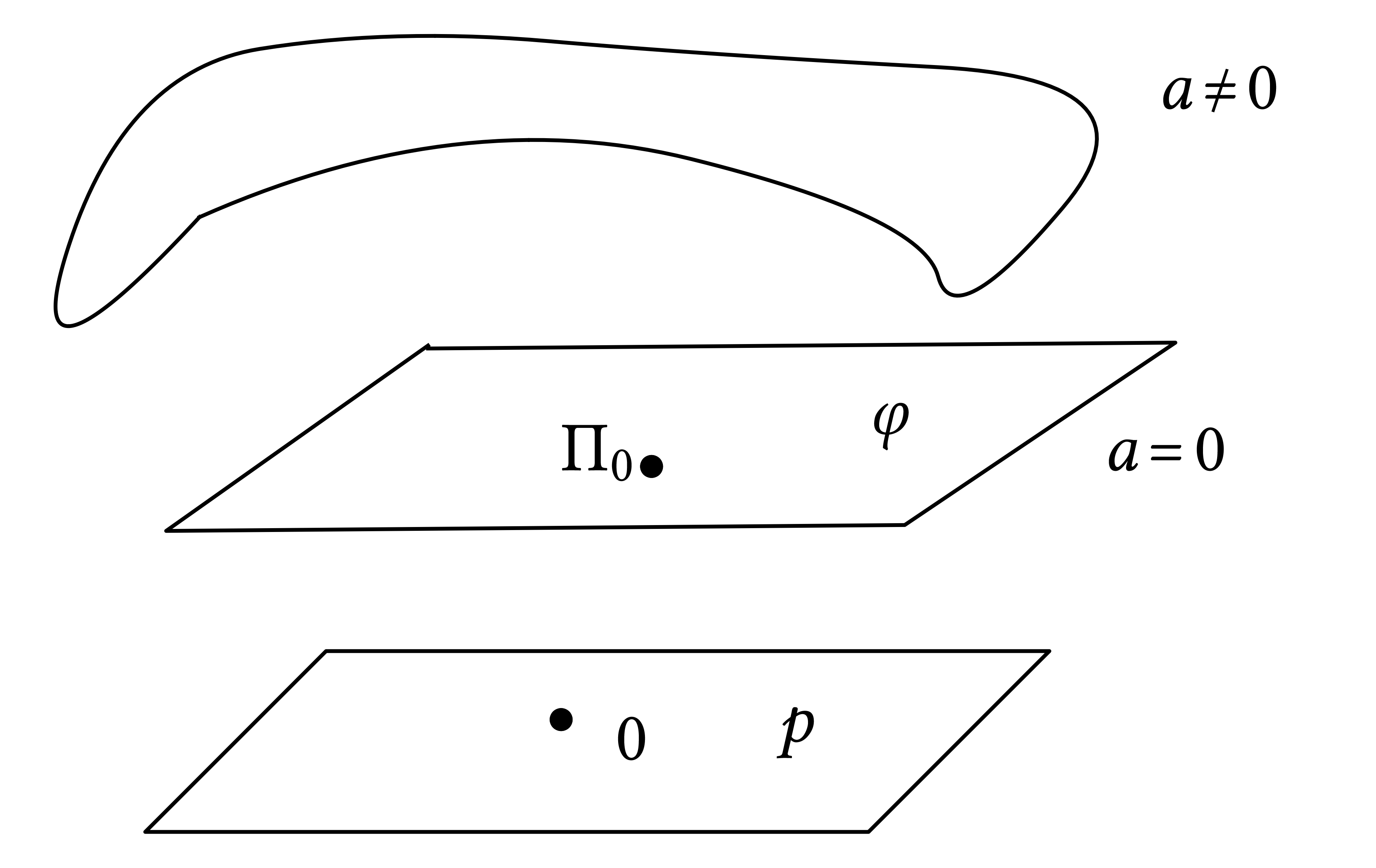
Goal: Extend this parametrization to neighborhood of \(a = 0\) in \(a\)-space in form of two maps \(\Pi [a, p], \Pi^- [a, p]\) such that
and
and s.t.
and
Otto | A cont. arg. in regularity structures | Lecture 1 | Tuesday July 22, 9:00–10:30
Plan: 1) Setup (informal ~ formal), definition of solutions; 2) A priori estimates on solutions; 3) Continuity argument to construct solutions.
1. Definition of solutions
1.1 Parametrization of solution manifold (informal)
To fix ideas consider an equation in the form
on \(\mathbb{R}^{1 + d} \in (y_0, y_1, \ldots, y_d)\) where \(L\) is a constant coefficients operator, maybe the heat operator \(L = \tfrac{\partial}{\partial y_0} - \tfrac{\partial^2}{\partial y_1^2} - \cdots - \tfrac{\partial^2}{\partial y_1^2}\) but it is not crucial and \(\xi\) is some distributional/analytic, and \(a (\varphi)\) is an analytic polynomial. We decide that we will solve the equation up to an analytic function \(q\):
this is not crazy since \(\xi\) and \(q\) are pretty much disjoint contributions. For \(a = 0\) the solution manifold
is an affine space over linear space of \(\{ p \shortmid L p \text{analytic} \} = \{ p \text{analytic} \}\). Pick a \(\Pi_0\) s.t. \(L \Pi_0 = \xi = \Pi_0^-\) then the map \(p \mapsto \Pi_0 + p\) is a parametrization of the solution manifold at \(a = 0\).
|
Goal: Extend this parametrization to neighborhood of \(a = 0\) in \(a\)-space in form of two maps \(\Pi [a, p], \Pi^- [a, p]\) such that and and s.t. and |
The condition \(\Pi^- = a (\Pi) + \Pi_0\) is not robust, and we will eventually replace it (in the last lecture).
Try implicit function argument. Let \(\delta \Pi^{(-)}\) denote the directional derivative of \(\Pi^{(-)}\) in directions of \(\delta a\) at \(a = 0\).
but this PDE leaves \(\delta \Pi\) underdetermined up to an analytic function.
Attempts to restrict the construction:
– translation invariance: \(\varphi (z + \cdot) = \hat{\varphi}\) and \(\xi (z + \cdot) = \hat{\xi}\) then \((\hat{\varphi}, \hat{\xi})\) is also a solution. Then we could try to impose covariance at the level of \(\Pi^{(-)}\), \(\Pi^{(-)} [a, p (z + \cdot)] = \hat{\Pi}^{(-)} [a, p] (z + \cdot)\) but this fails! Indeed look at \(d = 0\), \(\mathrm{d} \Pi_0 / \mathrm{d} x_0 = \Pi^-_0\) and think to \(\Pi^-\) as white noise and \(\Pi\) as Brownian motion and there is no way to impose this covariance.
– rescaling invariance: for \(r \in (0, \infty)\), let \(R y = (r^2 y_0, r y_1, \ldots, r y_d)\) is made s.t. \(L \{ y \mapsto \varphi (R y) \} = r^2 (L \varphi) (R \cdot)\), so if we rescale \(\varphi (R \cdot) = r^{\alpha} \hat{\varphi}\) and \(\xi (R \cdot) = r^{\alpha - 2} \hat{\xi}\) and \(a (r^{\alpha} \cdot) = r^{\alpha - 2} \hat{a}\) then \((\hat{a}, \hat{\varphi}, \hat{\xi})\) is again a solution. We can now try to impose that the parametrization of the solution manifold is covariant wrt. the scaling:
and this works! and fixrs the degree of non-uniqueness.
Range of \(\alpha\)? We want to be in the singular setting so \(\alpha < 0\), but we want also to be super-renormalizable, so we want \(a (\varphi) = r^{\alpha - 2} \hat{a} (r^{- \alpha} \varphi) \rightarrow 0\) as \(r \searrow 0\) so the l.h.s. \(O (r^{\alpha - 2 - K \alpha})\) [to finish] and this will give the condition \(\alpha > \cdots\).
1.2. Centered model \((\Pi, \Gamma)\) (informal)
No natural origin for space–time. \(\Pi^{(-)}_x\) for every origin = “base-point” \(x\). We recover covariance wrt. translations:
|
By construction, there exists such that and |
Covariance properties:
Remark.
— The big difference with RS is that we are more parcimonious on the parametrization of the objects, we reduce to the solution manifold and have the right amount of counterterms, the price to pay is that we are not able to formulate a linear fixpoint problem and we will use a continuity argument to handle the non-linear setting.
— There is no single canonical parametrization of the solution manifold, we have charts (caused by the choice of base-point) and transition maps given by the \(\Gamma\)s.
— We parametrize the rough manifold of solutions with analytic function (exploiting the property that they are indeed solutions).
1.3 Algebraization (informal to formal)
Recall informal:
Power-series Ansatz:
and \(\beta\) is a multi-index on index set \(\mathbb{N}_0 \sqcup \mathbb{N}_0^{1 + d}\) and \(\left( z^{\beta} := \prod_k z_k^{\beta (k)} \prod_n z_n^{\beta (n)} \right) [a, p]\).
we may construct these coefficients \(\Pi_{x \hspace{1em} \beta} \in \mathcal{S}' (\mathbb{R}^{1 + d})\). We put them in a single object as a formal power-series:
Polynomial sector: there are three classes of multi-indeces: 1) the polynomial ones,
and by construction in 1.1, (i.e. \(\Pi^- [a = 0, p] = \Pi^-_0\) and \(\Pi [a = 0, p] = \Pi_0 + p\)) we find
Recall 1.2 informally:
We make a power-series Ansatz
i.e. \(\Gamma_{x, x'}^{\star}\) is an algebra automorphism in the formal power series in the variables \(((z_k), (z_n))\) with coefficient in \(\mathbb{R}\):
By definition in 1.2. we get the axioms of regularity structures”
and this makes sense since \(\Pi_{x'}^{(-)} \in \mathcal{S}' [[z_k, z_n]]\) and \(\Gamma_{x, x'} \in \operatorname{End} (\mathbb{R} [[z_k, z_n]])\). The property \(\Gamma_{x, x'} [a, p] = (a, \ast)\) translates to the fact that \(\Gamma_{x, x'}^{\star} =\operatorname{id}\) on \(\mathbb{R} [[z_k]]\) and the scaling covariance translate to
with homogeneity
with \(| n | = 2 n_0 + n_1 + \cdots + n_d\).
Recall what \(\hat{\Pi}\) is. We rescale the solution and the parametrization of the solution manifold, and its coordinates
LOTT: We may construct \(\Pi_x \in \mathcal{S}' [[z_k, z_n]]\), \(\Gamma_{x, x'}^{\star} \in \operatorname{Aut} (\mathbb{R} [[z_n, z_k]])\) such that
1.4. Notion of solution (informal to formal)
point in \((a, p)\)-space which can be identified wth Dirac measures, which is nothing more than a multiplicative linear functionals on functions \(\pi\) on \((a, p)\) space. So it is convenient to think about this as an algebra homomorphism (character) of the algebra \(\mathbb{R} [[z_k, z_n]]\), i.e. \(\operatorname{Alg} (\mathbb{R} [[z_k, z_n]], \mathbb{R})\) and this is for us a modelled distribution.
Otto | Solution theory for singular SPDE | Lecture 2 | Tuesday July 22, 14:15–15:45
Recall our setting:
|
plus additional covariance properties of these objects. |
1.4 Notion of solution (informal to formal)
Fix a non-linearity \(a\).
Then \(\varphi = \Pi [a, p]\) for some \(p\) with \(L \Pi [a, p] = \Pi^- [a, p]\) \(\sim\) this is a point in \((a, p)\)-space \(=\) Dirac measure on \((a, p)\)-space \(=\) multiplicative functional on the space of functions on \((a, p)\)-space \(=\) an element \(f\) of the set of algebra homomorphism from \(\mathbb{R} [z_k, z_n]\) to \(\mathbb{R}\), i.e. \((f. \pi \pi') = (f. \pi) (f. \pi')\), \(f. 1 = 1\).
Recall that \(\mathbb{R} [z_k, z_n]\) is the space of polynomials, which in the dual picture give more freedom in \(\operatorname{Alg} (\mathbb{R} [z_k, z_n], \mathbb{R})\).
Ansatz: let's fix a base point \(x\) and let \(f_x \in \operatorname{Alg} (\mathbb{R} [z_k, z_n], \mathbb{R})\)
and
Could have taken a different base point \(x'\) and
We should think of \(f = (f_x)_x\) satisfying the covariance property
This is the space of “modelled distributions”. But there is a mistmatch also here between \(\mathbb{R} [z_k, z_n] \) and \(\mathbb{R} [[z_k, z_n]]\). We need a truncation to make these two structures compatible. Fix \(\kappa > 2\) and consider
defined as
Definition of a solution. A solution is a family \(f\) satisfying three conditions:
1. |
\(f = \{ f_x \in \operatorname{Alg} (R [z_k, z_n], \mathbb{R}) \}_x\) |
and
2. |
\(f_x .z_k = \frac{1}{k!} \frac{\mathrm{d}^k a}{d \varphi^k} (0), \qquad (f_{x'} - f_x . \Gamma_{x, x'})^{\gamma} = O (| x - x' |^{\kappa - | \gamma |})\) |
As a consequence of this condition and of the estimates of \(\Pi^{(-)}_x\) we have
and by reconstruction there exists unique (!) functions \(\varphi, \varphi^- \in \mathcal{S}'\) such that
now, for some \(\psi \in \mathcal{S}\):
and \(D = 2 + d\) is the effective dimension. And moreover we impose:
3. |
\(L \varphi = \varphi^-\) |
2. Apriori estimates of \(f\)
2.1 Overview
Fix \(\kappa > 2\) and \(\kappa \not{\in} \mathbb{N}\). Introduce norms
where recall that
and by construction in 1.1, (i.e. \(\Pi^- [a = 0, p] = \Pi^-_0\) and \(\Pi [a = 0, p] = \Pi_0 + p\)) we find
with \(\mathcal{B}\) a bounded set of Schwarz functions.
Auxiliary norms:
We can think to \(M\) as a \(C^{\kappa}\)-norm while to \(\| f \|\) as a \(C^{\lfloor k \rfloor}\)-norm, so slightly weaker. But these numbers refer to non-linear objects.
Four tasks:
1) Algebraic continuity argument: we can estimate \(M\) by \(M^{\operatorname{pol}}\) by a straighforward argument to get: |
2) Reconstruction: |
3) Integration: |
4) Three point argument |
All together these give
which looks quite good and useful, by taking \(\lambda\) small. To beat \((\| f \|)\) we need an interpolation argument. Estimate \(\| f \|\) as follows
but the real problem comes from the term \(C (\| f \|) \ast 1\) in the estimate for \(M\), this cannot be beaten easily.
We need a second round of estimates. Fix
define \(\tilde{M}, \tilde{M}^-, \tilde{M}^{\operatorname{pol}}, \tilde{R}, \tilde{R}^-\) with similar expressions as before.
Then \(\tilde{M}^-\) related to \(\gamma \in T^-\) with \(| \gamma | < \tilde{\kappa}\) are of the form \(\gamma (n) = 0\) for all \(n\) because \(\Gamma^{\star}_{x, x'}, f_x\) are “trivial” on \(z_k\)'s and \(\tilde{M}^- = 0\).
and the three steps above are:
Algebraic
Integration
three point argument
and all combined produce
and by periodic boundary conditions we have
and we can close the loop with a small constant \(\lambda\) in front of everything.
Let's go to some analytic estimates, e.g. for the algebraic argument
Lemma. a) For some \(\tilde{\kappa} < \kappa\)
Proof. Consider \(\gamma \in T^- = \{ 0 \} \cup \{ \gamma \shortmid \exists k, \gamma (k) \neq 0 \}\). If \(\gamma = 0\)
Now if \(\gamma (k) \neq 0\) for some \(k\) we write \(\gamma = \delta_k + \tilde{\gamma}\) and define a new \(\tilde{\kappa}\) by \(\kappa = (| \delta_k | - \alpha) + \tilde{\kappa}\) so that \(| \tilde{\gamma} | < \tilde{\kappa}\) and now with \(z^{\gamma} = z_k z^{\tilde{\gamma}}\) and use the properties of \(\Gamma^{\star}_{x, x'}\) to have
\(\Box\)
Otto | Solution theory for singular SPDEs | Lecture 3 | Wednesday July 24, 11:00–12:30
All we have already said in a picture:
solution manifold \(\{ \varphi \}\) |
param. via \((a, p)\)-space |
model |
modelled distr |
apriori estimates |
\(\{ \varphi | L \varphi = a (\varphi) + \xi + \text{analytic} \}\) |
(non robust) |
\(\Pi, \Pi^- \in \mathcal{S}' [[z_k, z_n]]\) \(\Pi [a, p] = \sum_{\beta} \Pi_{\beta} z^{\beta} [a, p]\) \(z^{\beta} = \Pi_{k \in \mathbb{N}_0} z_k^{\beta (k)} \Pi_{n \in \mathbb{N}_0^{1 + d}} z_n^{\beta (n)}\) |
\(f \in \operatorname{Alg} (\mathbb{R} [z_k, z_n], \mathbb{R})\) and |
Reconstruction Integration 3pt argument Algebraic argument |
\(\Pi_{\beta} = 0\) unless \(\beta \in T\) \(\Pi_{\delta_n (y)} = y^n\) for \(\delta_n = T^{\operatorname{pol}}\) \(\Pi_{\beta}^- = 0\) |
|
|
||
\(\varphi (R \cdot) = r^{\alpha} \hat{\varphi}\) \(\xi (R \cdot) = r^{\alpha - 2} \hat{\xi}\) \(a (r^{\alpha} \cdot) = r^{\alpha - 2} \hat{a}\) singular: \(\varphi \rightarrow \infty\) at fixed \(\hat{\varphi}\) super-rinorm \(\Leftrightarrow\) |
\(r^{| \beta |} \Pi_{\beta} = \hat{\Pi}_{\beta} (R \cdot)\) \(| \beta | - \alpha = \sum_{k \leqslant K} (\alpha k - (\alpha - 2)) \beta (k) + \sum_n (| n | - \alpha) \beta (n)\) as motivation for |
|
|
|
|
\(\Gamma_{x, x'}\) in \((a, p)\)-space to itself \(r^{\alpha} {}^{\backprime} \Gamma_{x 0} [a (r^{\alpha} \cdot), p (R \cdot)] = \hat{\Gamma}_{R x, 0}' [r^{\alpha - 2} a, r^{\alpha} p]\)
|
\(\Gamma^{\alpha}_{x, x'} \in \operatorname{Alg} (\mathbb{R} [[z_k, z_n]])\) \(\Gamma^{\star}_{x x'} =\operatorname{id}\) on \(\mathbb{R} [[z_k]]\)
\(r^{| \beta | - | \gamma |} (\Gamma^{\star}_{x 0})_{\beta}^{\gamma} = (\Gamma^{\star}_{R x 0})_{\beta}^{\gamma}\) |
\(f_x \in \operatorname{Alg} (\mathbb{R} [z_k, z_n], \mathbb{R})\) \(f_x .z_k = \frac{1}{k!} \frac{\mathrm{d}^k a}{d \varphi^k} (0)\) |
|
3. Existence via a continuity argument
Specify to \(a (\varphi) = \varphi^3\). Naively gives \(L \varphi = \varphi^3 + \xi\), but this has to be renormalized.
On the level of the model
which is an algebra.
Scaling property is destroyed by the regularisation, we replace it by saying
We drop the superscript \(\rho\).
Lemma. (consistency) If \(\varphi \in C^{\kappa}\) satisfies
then there exists a unique \(f = \{ f_x \in \operatorname{Alg} (\mathbb{R} [z_k, z_n], \mathbb{R}) \}_x\) such that
and
Classical result. Exists \(\varphi \in C^{\kappa}\) of \(L \varphi = \lambda \varphi^3 + h \varphi + \xi_{\rho}\) plus boundary conditions, and it is unique if it is not too large for \(| \lambda | \ll_{\rho} 1\). The bounds are not uniform in \(\rho\).
Strategy: monitor \(\dot{\varphi} = \frac{\mathrm{d} \varphi}{\mathrm{d} \lambda}\) and it satisfies
and establish solvability of
uniformly in \(| \lambda | \ll_{\Pi, \Gamma} 1\) then we are done, by a continuity argument.
Need a robust formulation of \(L_{\varphi} \dot{\varphi} = \zeta\).
means that \(\dot{f}\) is a derivation:
We then construct associated norms \(\dot{M}, \dot{R}, \ldots\)
Consider \(\dot{f} \in T_f \operatorname{Alg} (\mathbb{R} [z_k, z_n], \mathbb{R})\) with
and by reconstruction
we encode
by
Task: estimate \(M\) (norm of \(f\)) in terms of \([\zeta]_{\kappa - 2}\). This will require again the four arguments, but nothing more.
As in 2 we obtain apriori estimates in the linearized problem by running through the four tasks:
1) Algebraic argument (via the algebraic structure of the model distribution as the derivative of a coherent model distribution)
2) 3pt argument:
3) Integration
4) Reconstruction
5) Algebraic argument
and putting all together:
and \(\lambda \dot{M}\) can be absorbed, while \(\| \dot{f} \|\) can be interpolated using the argument of the previous lecture, to obtain for \(\lambda\) small depending only on \(\| \Pi, \Gamma \|\),
which allows to close the continuity argument only with the condition \(| \lambda | \ll 1 / \| \Pi, \Gamma \|\) which is stable for the passage to the limit.