SRQ seminar – September 24th, 2018

Notes from a talk in the SRQ series.

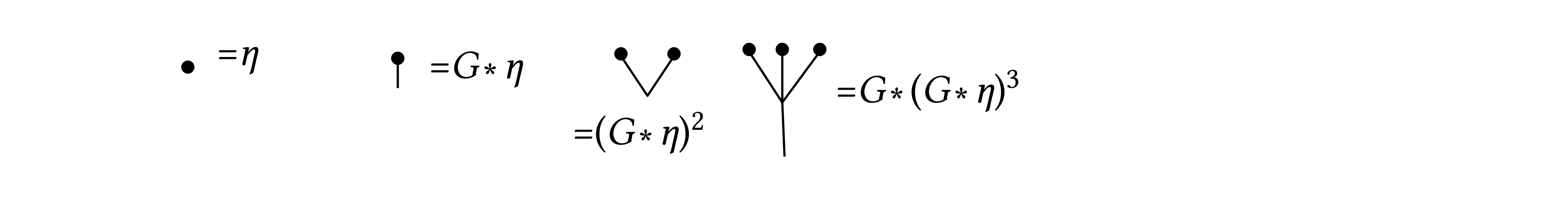
INI Seminar 20180924 Chandra

Parabolic scaling. $(t, x) \in \mathbb{R}^{d + 1}$. Distance $| (t, x) |_s := | t |^{1 / 2} + | x |$. Scales under $(t, x) \rightarrow (\lambda^2 t, \lambda x)$. Induces a metric on $\mathbb{R}^{d + 1}$ which has Hausdorff dimension $d + 2 = d_s$. We have

$\displaystyle \int_{| z |_s \leqslant 1} \frac{1}{| z |^{\alpha}_s} \mathrm{d} z < \infty \quad \text{iff $\alpha < d_s$} .$

Parabolic degree: if $q = (q_0, q_1, \ldots, q_d) \in \mathbb{N}^{d + 1}$ we define $| q |_s = 2 q_0 + q_1 + \cdots + q_d$ (time counts double).

Spaces $\mathcal{C}^{\alpha}_s$. For $\alpha > 0$, $\alpha \not{\in} \mathbb{Z}$ $f \in \mathcal{C}^{\alpha}_s$ if for all compact $\mathcal{K} \subseteq \mathbb{R}^{d + 1}$ we have

$\displaystyle \sup_{\text{\scriptsize{$\begin{array}{c} z, z' \in \mathcal{K}\\ | z - z' | \leqslant 1 \end{array}$}}} \frac{| f (z') - (T_z^{\lfloor \alpha \rfloor} f) (z') |}{| z - z' |_s^{\alpha}},$

where $T_z^n f (z')$ is the Taylor polinomial of $f$ centered around $z'$ of $(s)$-order $n$. Regularity for distributions: for $\alpha < 0$, $\alpha \not{\in} \mathbb{Z}$ $f \in \mathcal{C}^{\alpha}_s$ if

$\displaystyle \sup_{z \in \mathcal{K}} \frac{| f (\varphi_{\lambda, z}) |}{\lambda^{\alpha}} < \infty$

where $\varphi_{\lambda, (t, x)} (t', x') = \lambda^{- d - 2} \varphi (\lambda^{- 2} (t' - t), \lambda^{- 1} (x' - x))$ for a suitable class of test functions $\varphi$ and $\lambda \in (0, 1]$.

Multiplication theorem. There exists a bilinear form $\mathcal{C}^{\alpha}_s \times \mathcal{C}^{\beta}_s \rightarrow \mathcal{C}^{\alpha \wedge \beta}_s$ which extends the canonical multiplication of smooth functions iff $\alpha + \beta > 0$.

Scaling is motivated by looking at problems involving the heat operator $\partial_t - \Delta$.

$\displaystyle G (z) = (\partial_t - \Delta)^{- 1} (z) .$

Then $G$ is smooth away from $z = 0$ and near $z = 0$ we have $| \mathrm{D}^j G (z) | \lesssim | z |_s^{2 - d_s + | j |_s}$ with any multiindex $j \in \mathbb{N}^{d + 1}$.

Classical Schauder estimate. Convolution with $G$ improves regularity by 2 mapping $\mathcal{C}^{\alpha}_s$ in $\mathcal{C}^{\alpha + 2}_s$, this is the main reason to introduce parabolic scaling.

(sketch of proof) “Localization”. One can write the heat kernel $G$ as $G = K + R$ such that $R$ is smooth and $K$ is zero in $| z |_s > 1$ and agrees with $G$ in $| z |_s \leqslant 1 / 2$ and has a certain number of vanishing moments, namely:

$\displaystyle \int K (z) z^{\ell} \mathrm{d} z = 0 \quad \text{for $| \ell |_s < \alpha$} .$

Given $f \in \mathcal{C}^{\alpha}_s$, want to show that $K \ast f \in \mathcal{C}^{\alpha + 2}_s$. Assume $\alpha > 0$, for $j \in \mathbb{N}^{d + 1}$

$\displaystyle \int \underbrace{\mathrm{D}^j K (z - y)}_{\sim | z |_s^{2 - d_s - | j |_s}} f (y) \mathrm{d} y = \int \mathrm{D}^j K (z - y) \underbrace{(f (y) - (T_z^{\lfloor \alpha \rfloor} f) (y))}_{| y - z |^{\alpha}_s} \mathrm{d} y$

which is ok if $2 - | j |_s + \alpha > 0$. This proves the theorem. We can sneak in the Taylor expansion due to the moment condition of $K$.

When $\alpha < 0$ we decompose the singular kernel as an (infinite) sum of smooth pieces and evaluate the degree of divergence of each term.

Kolmogorov criterion. (for the Hölder–Besov spaces). Let $\theta \leqslant 0$, $p > 1$, $\alpha < 0$. Assume we are given a random element $g \in \mathcal{S}' (\mathbb{R}^{d + 1})$ for which, given any compact $\mathcal{K} \subset \mathbb{R}^{d + 1}$

$\displaystyle \sup_{\text{\scriptsize{$\begin{array}{c} z \in \mathcal{K}\\ \text{suitable $\varphi$}, \lambda \in (0, 1] \end{array}$}}} \frac{\mathbb{E} [| g (\varphi_{\lambda, z}) |^p]}{\lambda^{\theta p}} < \infty .$

Then for any $\alpha < \theta - \frac{d + 2}{p}$, $g$ admits a version in $\mathcal{C}^{\alpha}_s$. This is important to obtain the key probabilistic features of random distributions to be used as input in the deterministic analysis.

Important fact: equivalence of moments. There exists constants $c_p$ (for $p \geqslant 1$) such that for any Gaussian random variable $X$

$\displaystyle \mathbb{E} [| X |^p] \leqslant c_p (\mathbb{E} [| X |^2])^{p / 2}$

(by direct computation). But it also holds for objects in Wiener chaoses / Hermite polinomials / Wick powers. In particular the behaviour of the second moments is enough to get the Kolmogorov criterion working by having arbitrary large $p$ and therefore construct versions which are in $\mathcal{C}^{\theta - \varepsilon}_s$ for any small $\varepsilon > 0$.

For example if $\eta$ is space–time white noise then $\mathbb{E} | \eta (\varphi_{\lambda, z}) |^2 = \lambda^{- d_s} = \lambda^{- d - 2}$ and using equivalence of moments and the Kolmogorov criterion we can prove that $\eta \in \mathcal{C}^{- d / 2 - 1 -}_s$ where $\theta -\!\!= \theta - \kappa$ for some fixed arbitrary small $\kappa > 0$.

Diagrammatic notation. $\bullet := \eta$

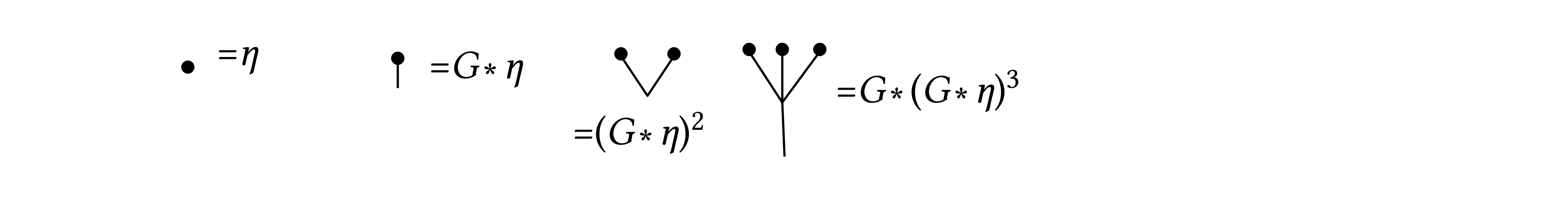
And if we introduce a $\delta$–sequence $\rho_{\varepsilon} \rightarrow \delta$ as $\varepsilon \rightarrow 0$ then we denote with $\bullet_{\varepsilon} := \eta$ and etc.. the associated objects.

Wick powers. $\rho_{\varepsilon} \ast G \ast \eta \rightarrow G \ast \eta$ as $\varepsilon \rightarrow 0$ for every realization of $\eta$. But $(\rho_{\varepsilon} \ast G \ast \eta)^3$ does not converge in any reasonable sense.

[(Note from the redactor) Computations with trees follows which I'm not able to reproduce right now, It is shown how uniform bounds on $(G \ast \eta_{\varepsilon})^2$ can be obtained if we remove the average and consider instead $Y_{\varepsilon} := (G \ast \eta_{\varepsilon})^2 - c_{\varepsilon}$ where $c_{\varepsilon} = (G \ast \eta_{\varepsilon})^2 (0)$. The renormalized product $Y_{\varepsilon}$ is shown to converge in $\mathcal{C}^{- d_s + 4 -}_s$]

When $d = 2$ $Y \in \mathcal{C}^{0 -}$. Similarly $Z_{\varepsilon} := (G \ast \eta_{\varepsilon})^3 - c_{\varepsilon}' (G \ast \eta_{\varepsilon})$ converges to $Z \in \mathcal{C}^{(- 3 d_s + 12) / 2 -}$ but only for $2 \leqslant d < 4$. At $d = 4$ the regularity of this object start to ressemble as the space–time white noise. Again when $d = 2$ we also have $Z \in \mathcal{C}^{0 -}$.

Da Prato–Debussche argument. (applied to $\Phi^4_2$) We consider the equation

$\displaystyle (\partial_t - \Delta) u = - u^3 + \eta,$

in $[0, T] \times \mathbb{T}^d$ (not in $\mathbb{R}^{d + 1}$) and we allow (for the moment) for blowup of solutions. Namely I start from an initial data and a realization of the noise and we are looking for the small time solutions of this problem thinking about it as a fixpoint problem (in the mild formulation):

$\displaystyle u = G \ast (- u^3 + \eta) .$

We have $X_{\varepsilon} := G \ast \eta \in \mathcal{C}^{0 -}$. This means that at best $u \in \mathcal{C}^{0 -}$ but this poses problems to define $u^3$. If we regularise we have

$\displaystyle (\partial_t - \Delta) u_{\varepsilon} = - u^3_{\varepsilon} + \eta_{\varepsilon},$

and everything is fine. But as we take $\varepsilon \rightarrow 0$ the solutions $u_{\varepsilon}$ will not converge in any reasonable sense. The solution map $\eta_{\varepsilon} \mapsto u_{\varepsilon}$ is not continuous in the topology where $\eta_{\varepsilon} \rightarrow \eta$. We need also to renormalize, that is change the equation into

$\displaystyle (\partial_t - \Delta) u_{\varepsilon} = - (u^3_{\varepsilon} - 3 c_{\varepsilon} u_{\varepsilon}) + \eta_{\varepsilon} .$

As $\varepsilon \rightarrow 0$ the solution should look like the solution of the linear problem $u_{\varepsilon} \sim (G \ast \eta_{\varepsilon}) =: X_{\varepsilon}$ and we are just mimicking the form of the third Wick polynomial. So we write $u_{\varepsilon} = X_{\varepsilon} + v_{\varepsilon}$, then

$\displaystyle (\partial_t - \Delta) v_{\varepsilon} = - \underbrace{(X^3_{\varepsilon} - 3 c_{\varepsilon} X_{\varepsilon})}_{\mathbb{X}^3_{\varepsilon}} - 3 \underbrace{(X^2_{\varepsilon} - c_{\varepsilon})}_{\mathbb{X}^2_{\varepsilon}} v_{\varepsilon} - X_{\varepsilon} v_{\varepsilon}^2 - v_{\varepsilon}^3 .$

Now, working in the limit $\varepsilon \rightarrow 0$, we have $\mathbb{X}_{\varepsilon}^3 \rightarrow \mathbb{X}^3$ and $\mathbb{X}_{\varepsilon}^2 \rightarrow \mathbb{X}^2$ in $\mathcal{C}^{0 -}_s$. Then we can consider the equation

$\displaystyle (\partial_t - \Delta) v = -\mathbb{X}^3 - 3\mathbb{X}^2 v - X v^2 - v^3,$

and write it in the mild formulation as

$\displaystyle v = G \ast (-\mathbb{X}^3 - 3\mathbb{X}^2 v - X v^2 - v^3) .$

Now $G \ast \mathbb{X}^3 \in \mathcal{C}^{2 -}$ by Schauder theory. Therefore, we can try to assume that $v \in \mathcal{C}^{2 -}$ and in this case both the products $\mathbb{X}^2 v$ and $X v$ are well defined since $\mathbb{X}^2, X \in \mathcal{C}^{0 -}$using the multiplication theorem. Moreover we know that $\mathbb{X}^2 v, X v \in \mathcal{C}^{0 -}$ again by the multiplication theorem's estimates. Therefore the assumption $v \in \mathcal{C}^{2 -}$ is indeed consistent with the form of the equation and makes a well defined fixpoint problem in $\mathcal{C}^{\alpha}$ for any $\alpha \in (0, 2)$. It has a unique local solution in $[0, T]$ for some small $T$ which depends on the size of $X, \mathbb{X}^2, \mathbb{X}^3$. The map is continuous from the new random data $(X, \mathbb{X}^2, \mathbb{X}^3)$ to the solution of the equation $v = V (X, \mathbb{X}^2, \mathbb{X}^3)$. By continuity we obtain that $v_{\varepsilon} = V (X_{\varepsilon}, \mathbb{X}^2_{\varepsilon}, \mathbb{X}^3_{\varepsilon}) \rightarrow V (X, \mathbb{X}^2, \mathbb{X}^3) = v$ by continuity and convergence of the random triplet $(X, \mathbb{X}^2, \mathbb{X}^3)$. Note that $\eta \mapsto (X, \mathbb{X}^2, \mathbb{X}^3)$ is not a continuous map.

In $d = 3$ this arguments breaks down (in this simplicity). Indeed there $\mathbb{X}^2 \in \mathcal{C}^{- 1 -}$ and on the r.h.s you alway have a term of the form $\mathbb{X}^2 v \in \mathcal{C}^{- 1 -}$ which forces $v$ to be in $\mathcal{C}^{1 -}$ but this insufficient to define this very same product. This hints that this notion of regularity is not appropriate to handle this equations, there are divergences which span multiple orders of perturbation theory and can be tackled by this simple analytical setup.