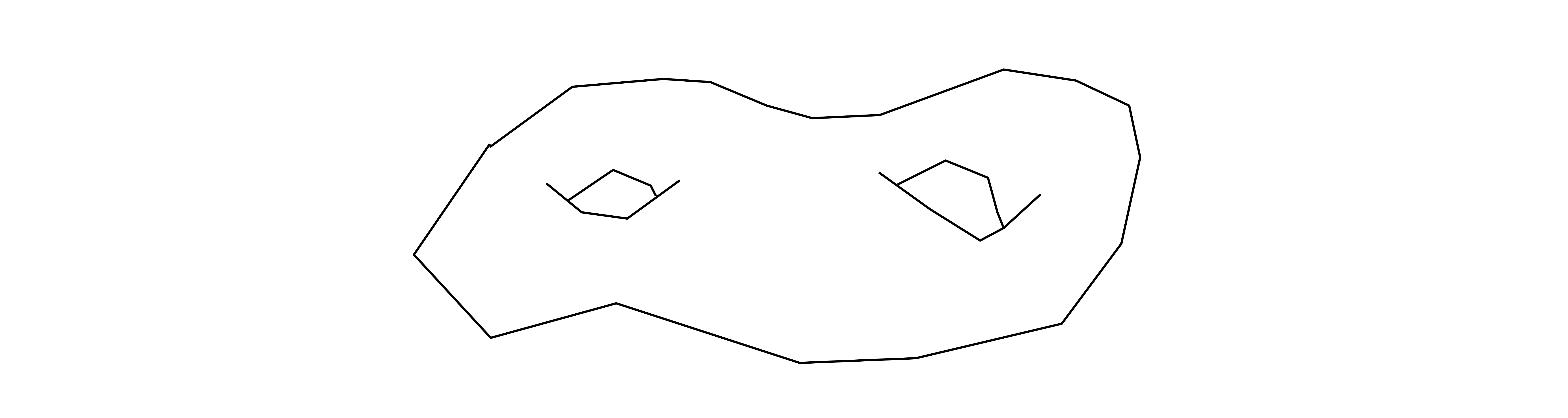
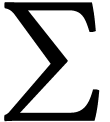 a compact surface or
a compact surface or  . We need areas, so we consider a volume form on
. We need areas, so we consider a volume form on
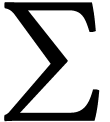 .
. 
INI Seminar/Talk 20181003 T. Levy
2d Yang–Mills holonomy process
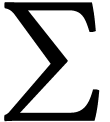 a compact surface or
a compact surface or  . We need areas, so we consider a volume form on
. We need areas, so we consider a volume form on
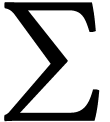 .
. 
 a compact Lie group, connected.
a compact Lie group, connected.  a Lie algebra with scalar product
a Lie algebra with scalar product  .
Example
.
Example 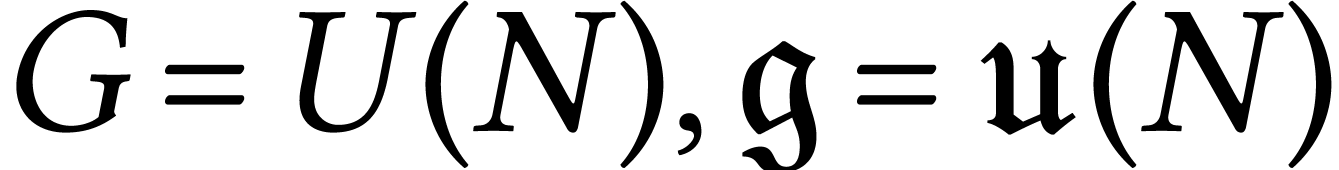 and
and 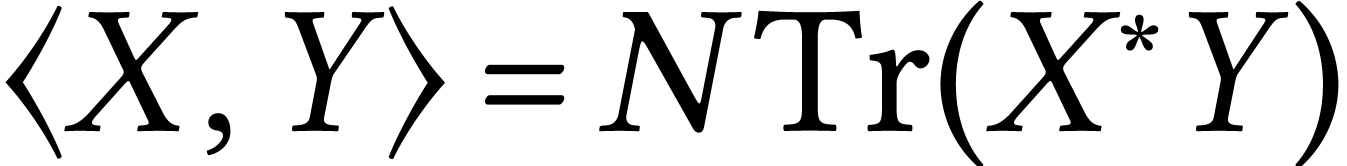 .
.
 connections on the principal bundle
connections on the principal bundle  .
.
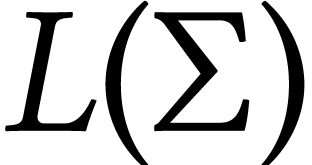 : continuous loops on
: continuous loops on 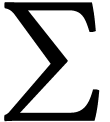 with finite length, up to re-param. (finite lenght is
a diffeo invariant notion).
with finite length, up to re-param. (finite lenght is
a diffeo invariant notion).
We want to describe a collection of  –valued
random variables
–valued
random variables 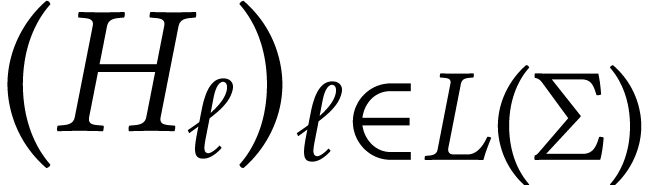 such that their distribution is
heuristically given by
such that their distribution is
heuristically given by

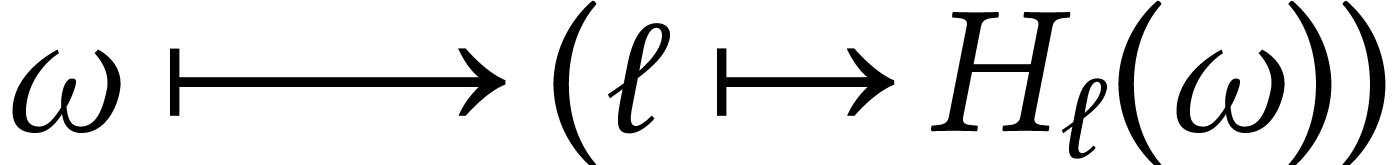
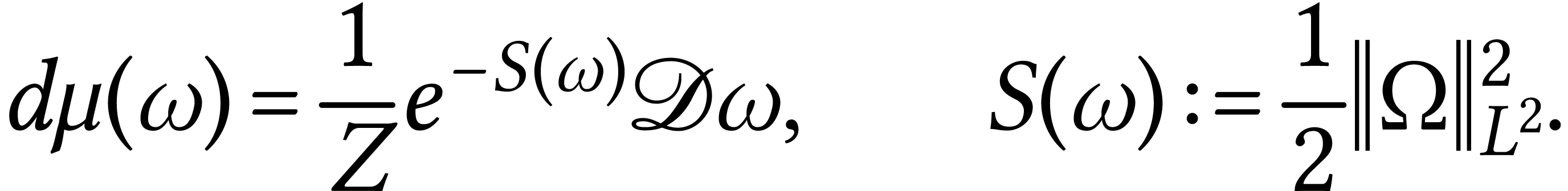
This is a probability measure on ( –valued)
–valued)
 -forms on the manifold
-forms on the manifold 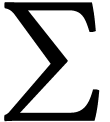 which is invariant under certain transformations.
which is invariant under certain transformations.
Multiplicativity
If 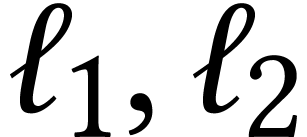 are two loops based on the same point then we
must have
are two loops based on the same point then we
must have
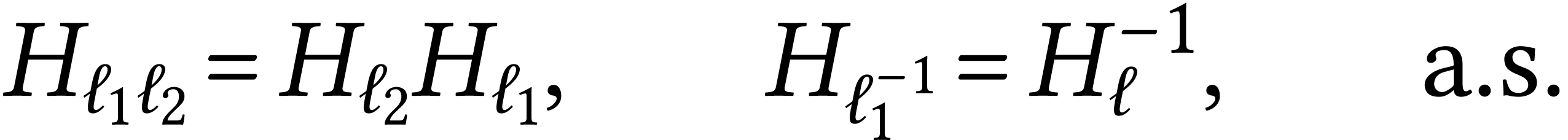
where 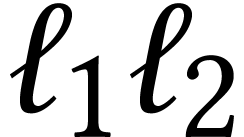 is the concatenation of the two loops and
is the concatenation of the two loops and
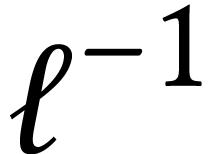 is the loop run in opposite sense.
is the loop run in opposite sense.
The curvature 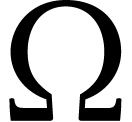 of the random connection is
distributed like white noise. Since curvature controls the infinitesimal
holonomies we should expect this to show up in
of the random connection is
distributed like white noise. Since curvature controls the infinitesimal
holonomies we should expect this to show up in 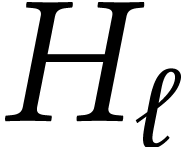 .
.
We imagine: 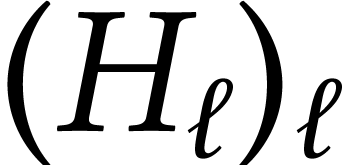 is Brownian motion/bridge on
is Brownian motion/bridge on  indexed by
indexed by 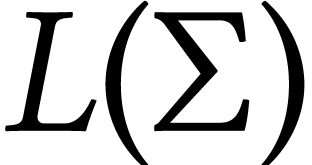 with the area
playing the role of time.
with the area
playing the role of time.
Lattice Yang–Mills theory
(Finite dimensional marginals of the holonomy process)
We start from our surface  and discretize it by
drawing a graph
and discretize it by
drawing a graph  over it (e.g. a triangulation).
It is a real embedded graph.
over it (e.g. a triangulation).
It is a real embedded graph. 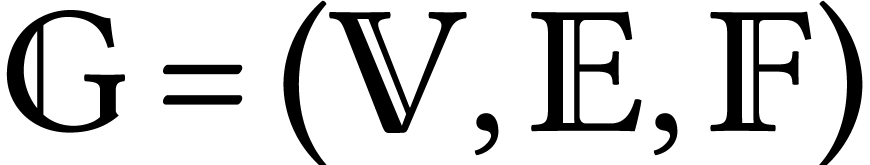 where
where  are points of the surface and
are points of the surface and  which are edges embedded in the surface. Therefore it has faces
which are edges embedded in the surface. Therefore it has faces  . (we assume orientation for each
edge in
. (we assume orientation for each
edge in  )
)
Configuration space 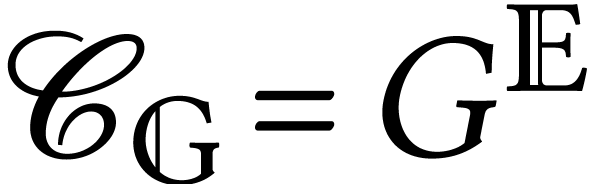 . Let
. Let
 be a path in
be a path in  ,
that is
,
that is 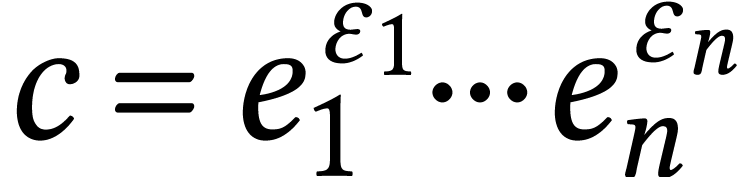 :
: 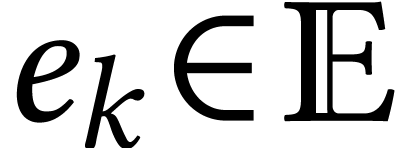 and
and 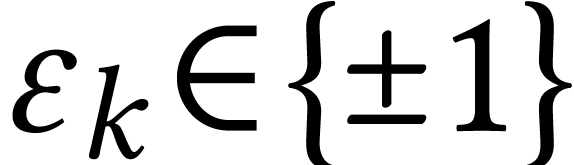 an orientation. Then we consider the
discrete holonomy
an orientation. Then we consider the
discrete holonomy

This is a discrete version of a connection. There is a natural
probability measure on  by taking the product
measure of Haar measure on
by taking the product
measure of Haar measure on  .
To make it more interesting we take the heat kernel on
.
To make it more interesting we take the heat kernel on  :
:

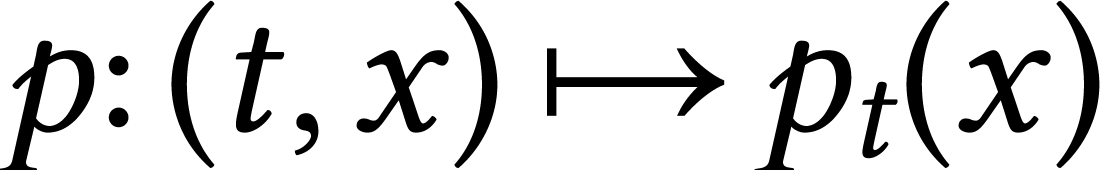
fundamental solution of the heat equation
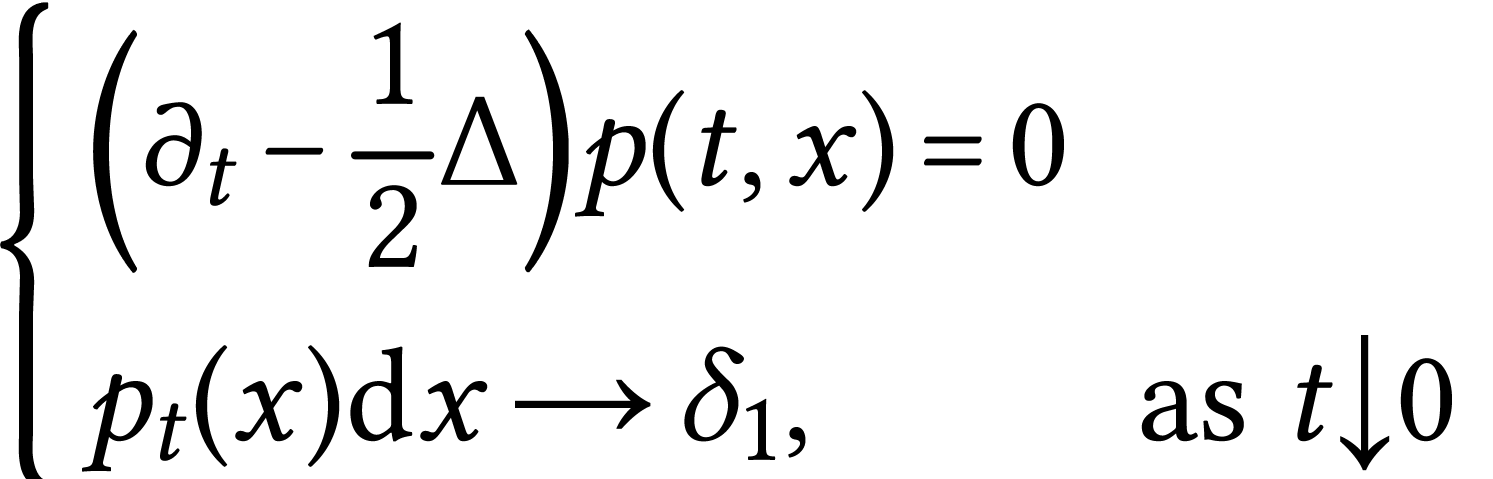
It satisfies
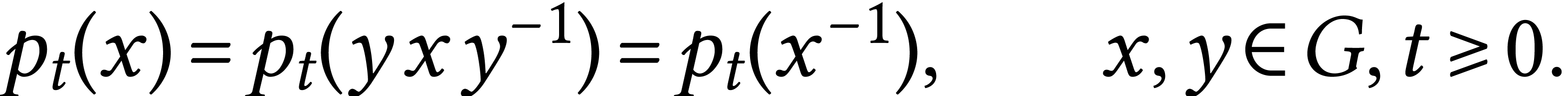
Sengupta's formula (Migdal, Witten, Driver)
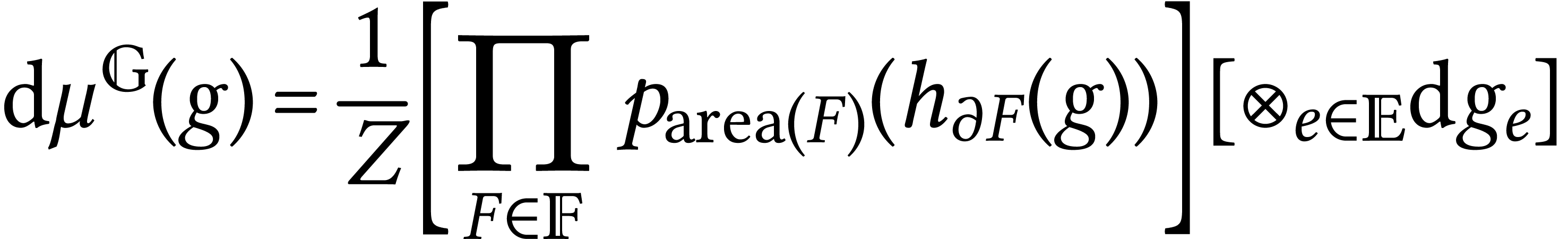
This expression has the advantage that it gives a consistent family of probability measures, namely it is invariant under subdivisions.
Consider two graphs, 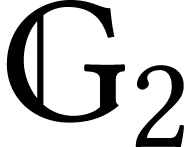 finer than
finer than 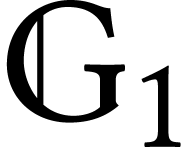 . We have a natural map
. We have a natural map 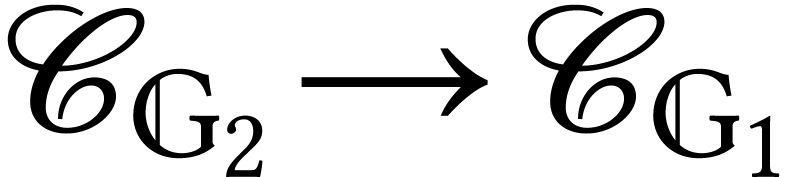 by decimation which preserves the measure:
by decimation which preserves the measure: 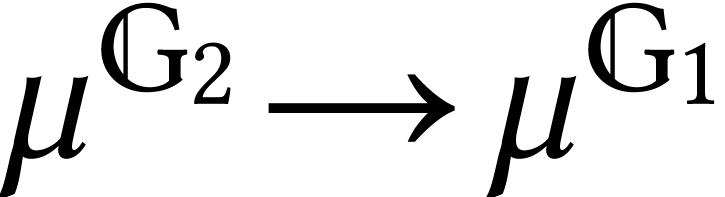 .
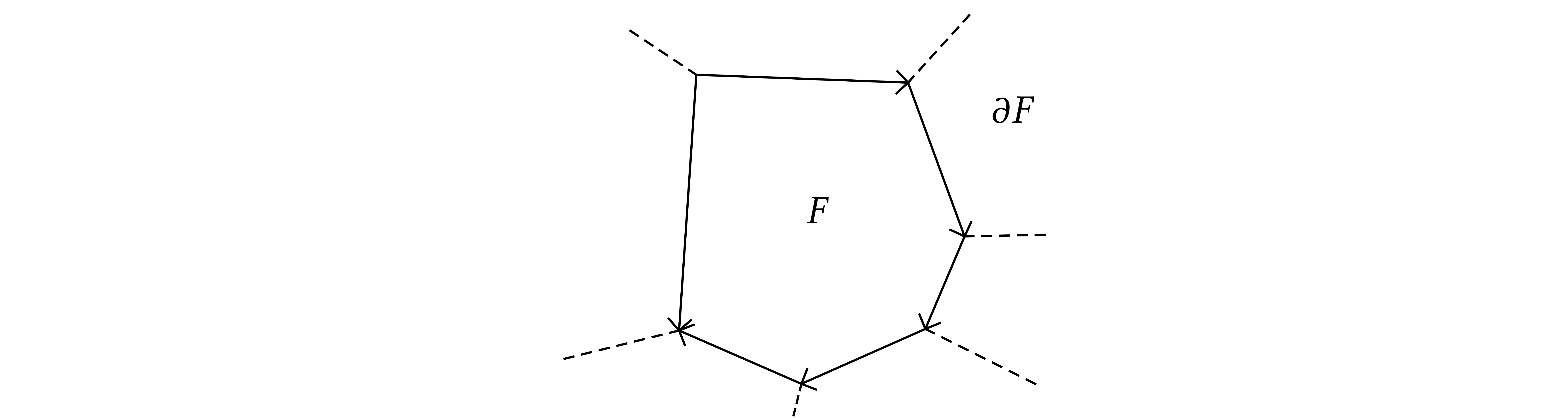
Consider a face
.
Consider a face  of
of  which
is split in two in
which
is split in two in  as in this figure:
as in this figure:
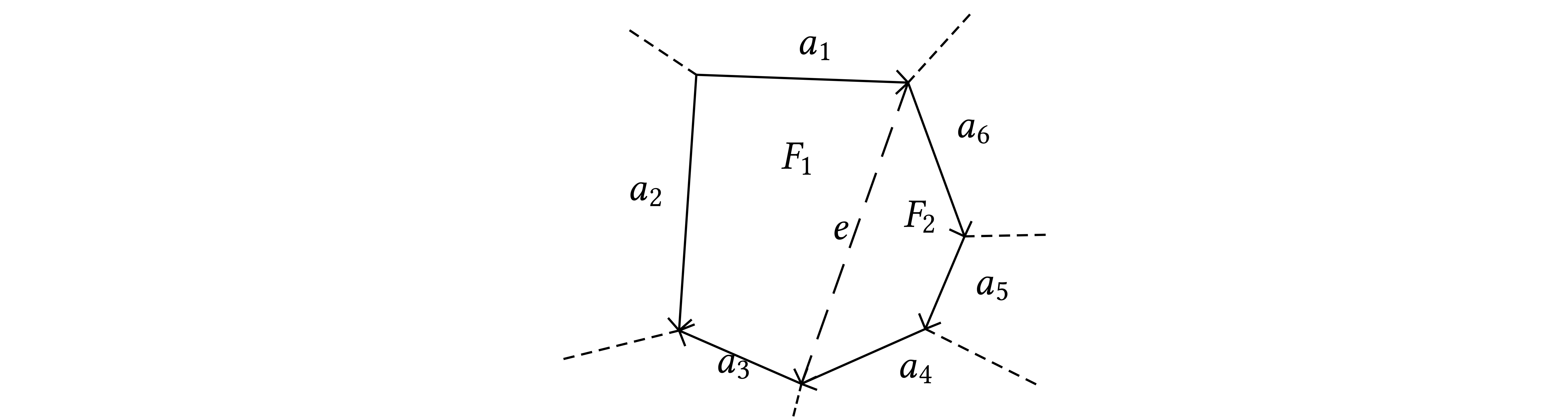
Here  . Now
. Now 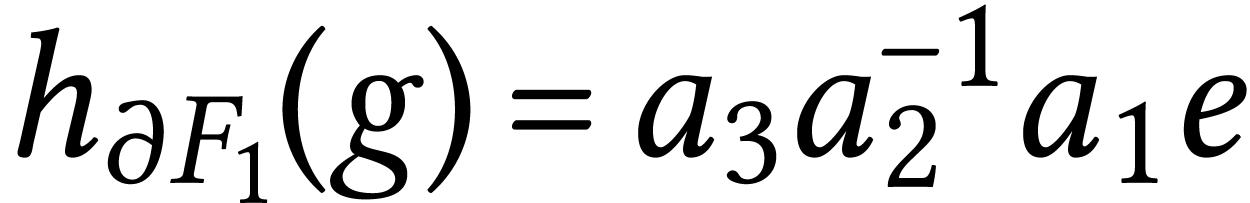 and
and 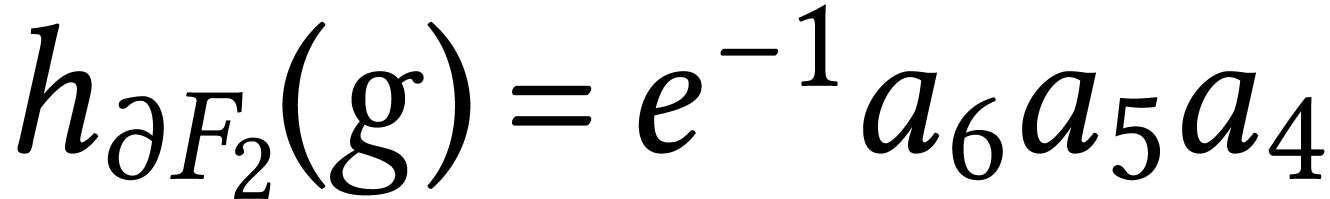 ,
,  and
and 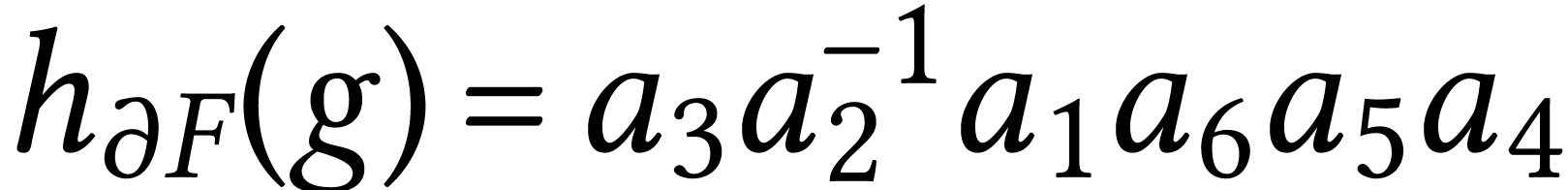 . The convolution of the
heat–kernel allows for the following computation
. The convolution of the
heat–kernel allows for the following computation
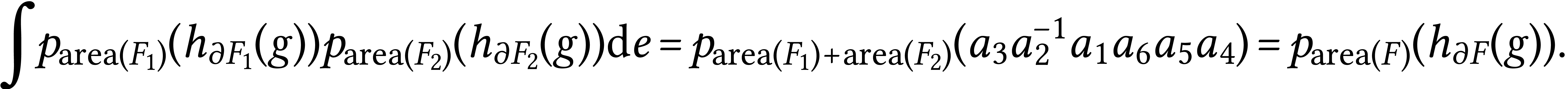
This is the reason to use the heat kernel in the definition of 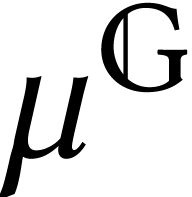 .
.
Theorem 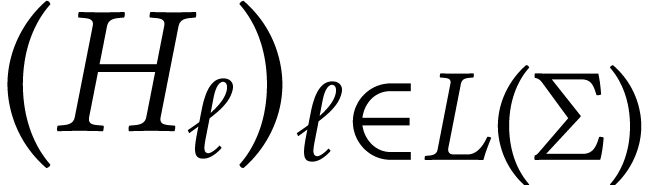 of
of  -valued
r.v.s, unique in distribution, which is consistent with the lattice
theory and stochastically continuous.
-valued
r.v.s, unique in distribution, which is consistent with the lattice
theory and stochastically continuous.
Ilya Chevyrev has a recent preprint where he defines a space of
distributional connections  on which he is able
to define a probability measures and holonomies whose law coincide with
the holonomy process.
on which he is able
to define a probability measures and holonomies whose law coincide with
the holonomy process.
Example 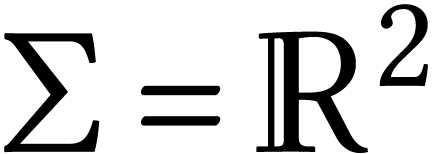 . Two loops
. Two loops 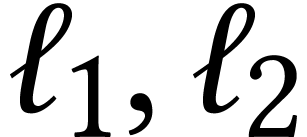 with disjoint
areas of size
with disjoint
areas of size 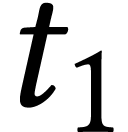 and
and 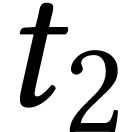 ,
then
,
then
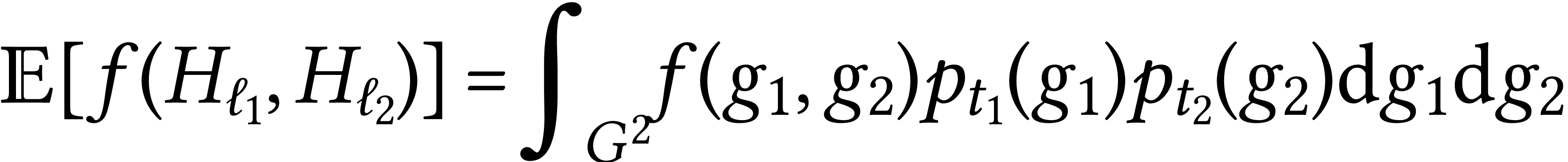
so 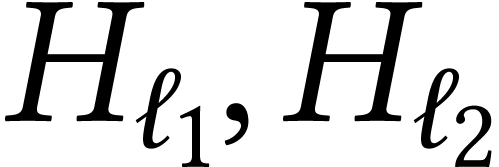 are independent and distributed like the
Brownian motion on
are independent and distributed like the
Brownian motion on  at time
at time 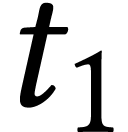 and
and 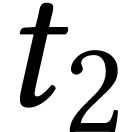 . If the two loops have
non disjoint areas then we can write them as three loops
. If the two loops have
non disjoint areas then we can write them as three loops 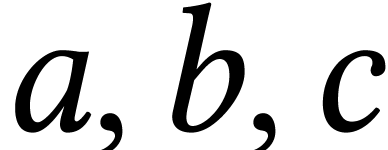 with disjoint areas of size
with disjoint areas of size 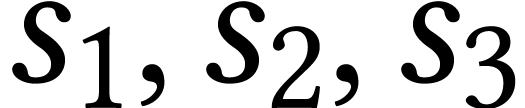 such
that
such
that 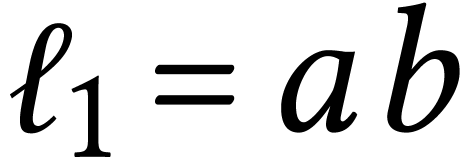 ,
, 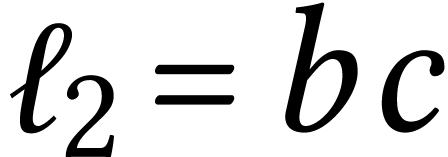 and now
and now
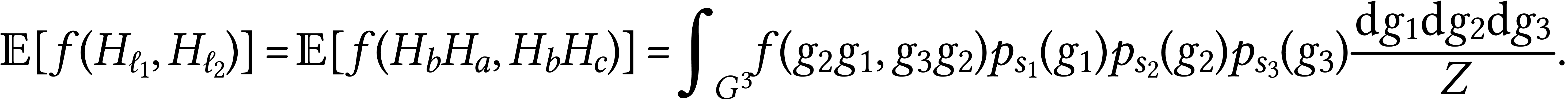
Example  with area
with area  . Two loops
. Two loops 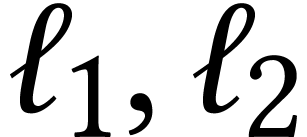 with disjoint areas of size
with disjoint areas of size 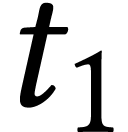 and
and 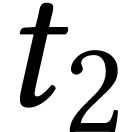 . Then outside there is
third face of area
. Then outside there is
third face of area 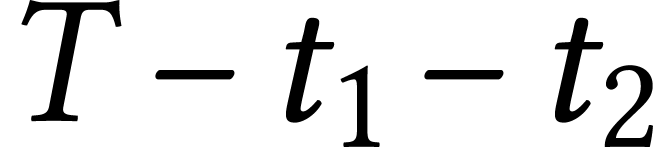 . In this
case Sengupta's formula gives:
. In this
case Sengupta's formula gives:
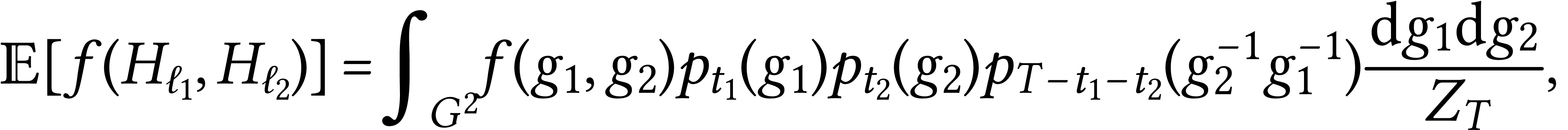
with 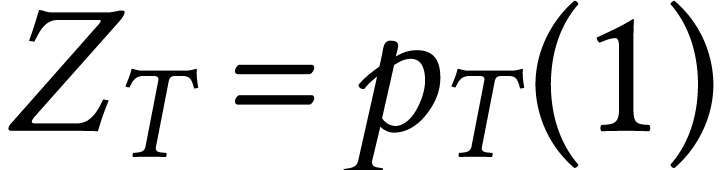 . So now
. So now 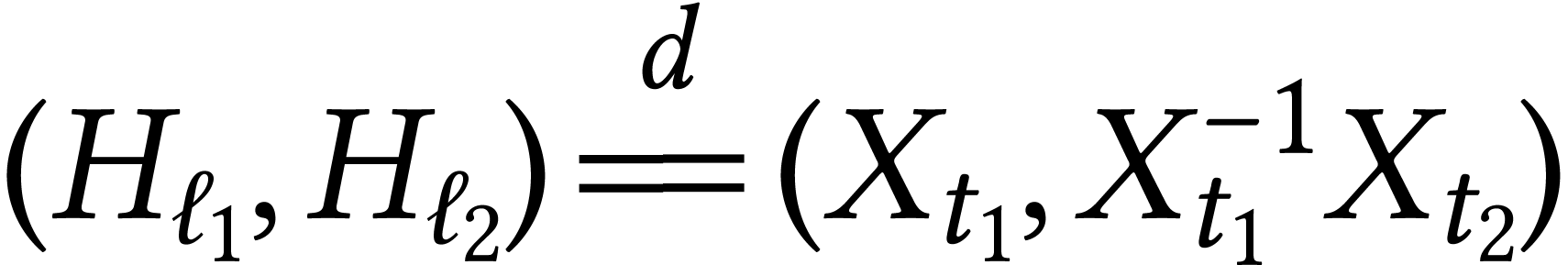 where
where  is a Brownian bridge on
is a Brownian bridge on  conditioned to return to
conditioned to return to  at
time
at
time  .
.
The large N limit.
We consider expectations of Wilson's loops:
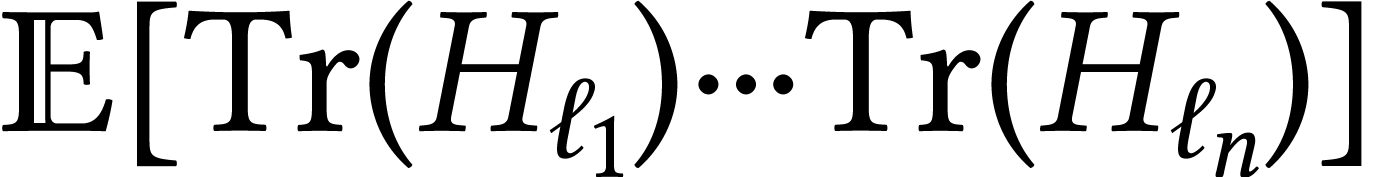
We are going to do some simple computations of numbers of this kind which reveal some combinatorical phenomena which will “resurface” also in MM equations.
Take  .
. 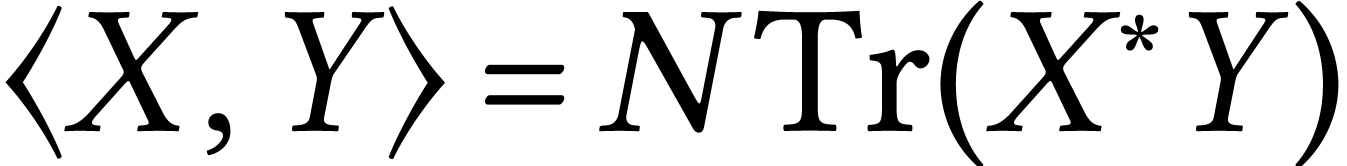 .
. 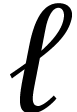 a loop of area
a loop of area 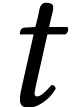 on
on 
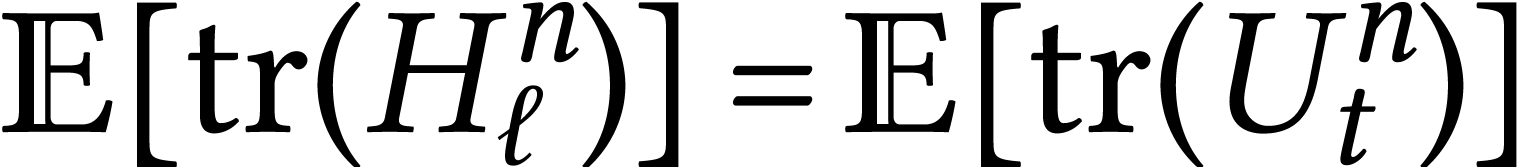
where 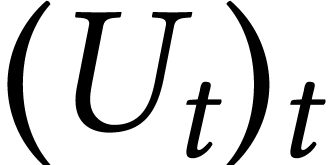 is the Brownian motion on
is the Brownian motion on 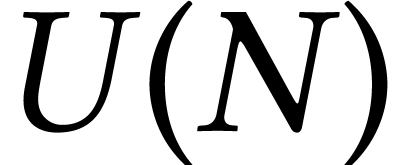 . We use the notation
. We use the notation  (normalized trace) so that
(normalized trace) so that 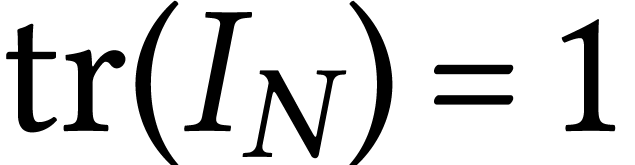 .
.
The BM on 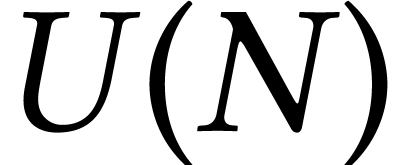 is given by an SDE. Take a linear
Brownian motion
is given by an SDE. Take a linear
Brownian motion 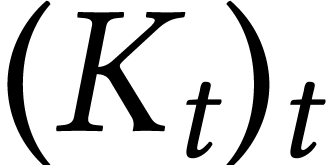 on
on 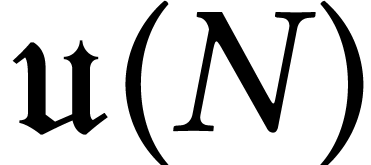 such
that
such
that
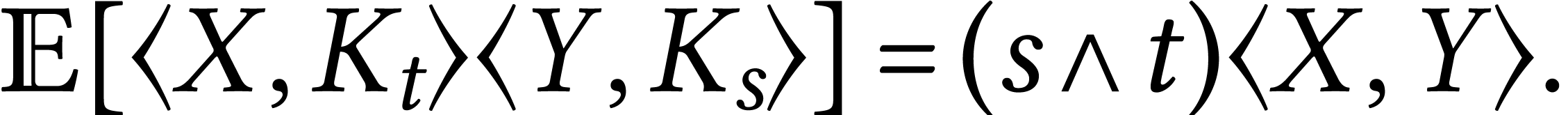
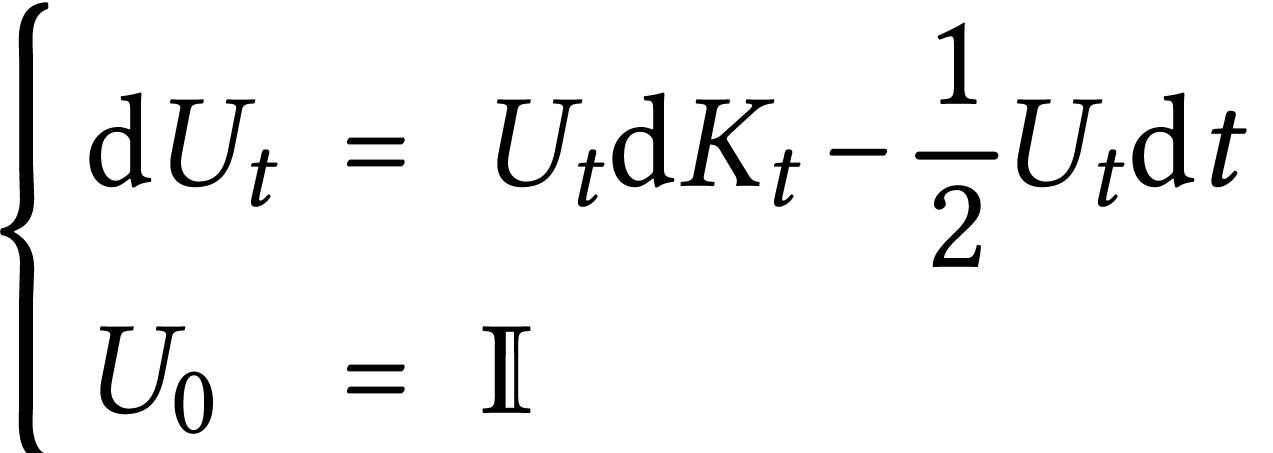
Given this we can compute
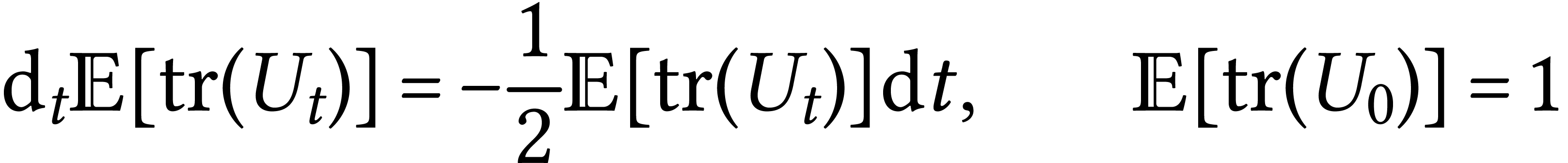
so
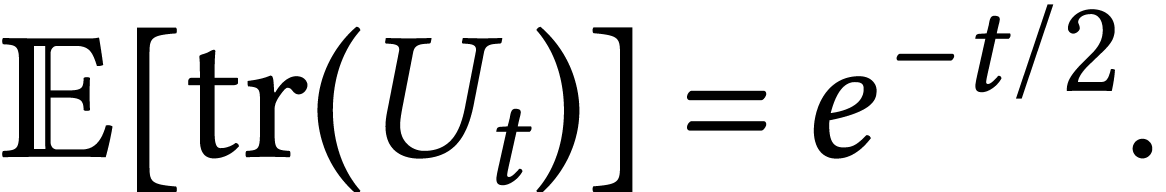
Let us try to compute
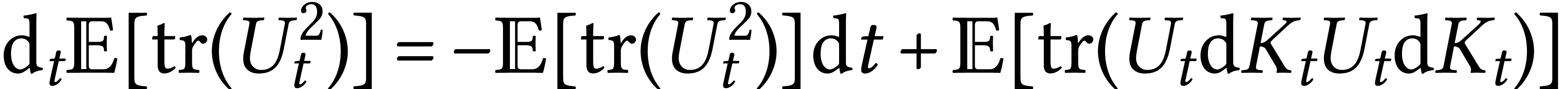
In order to compute 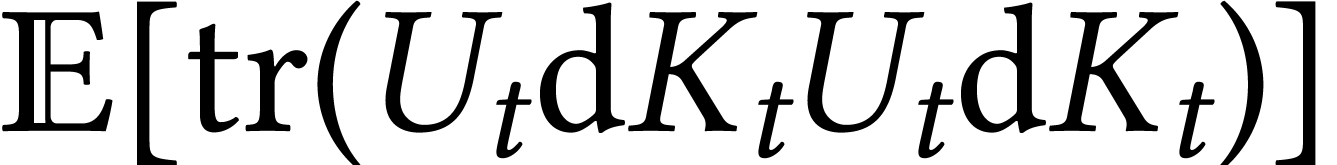 we take an ONB
we take an ONB 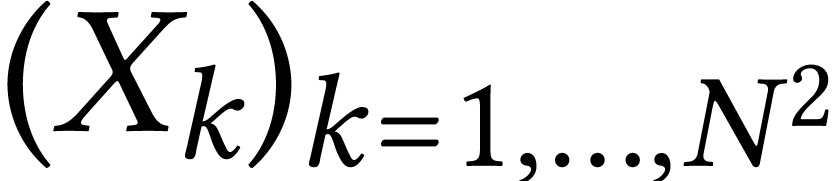 of
of 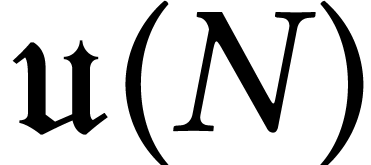 and we say that
and we say that 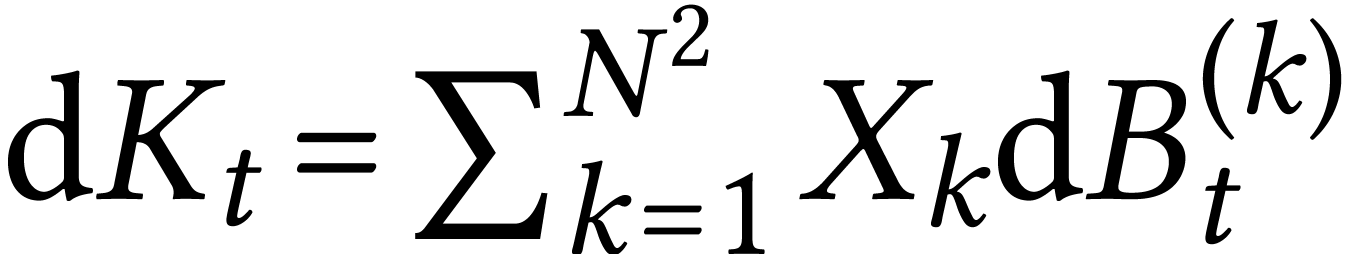 . We therefore conclude that
. We therefore conclude that
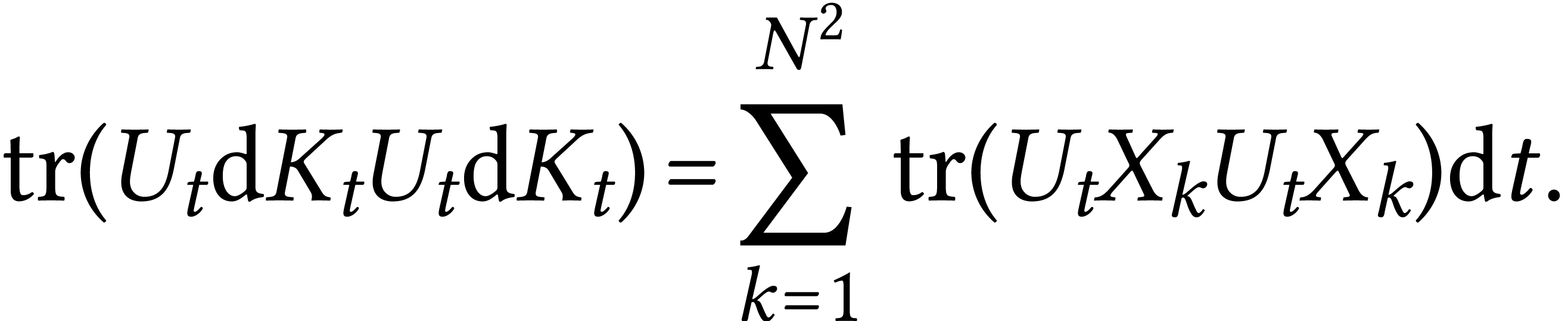
We use now the following identity
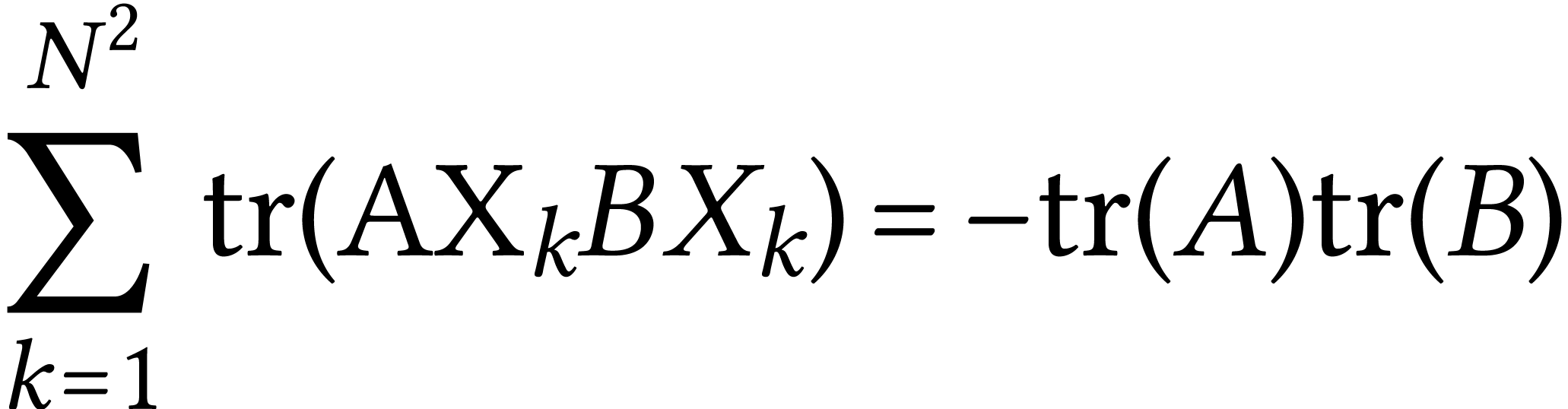
which is proven by proving first that it does not depend on the basis and then using your preferred basis to do the computation.
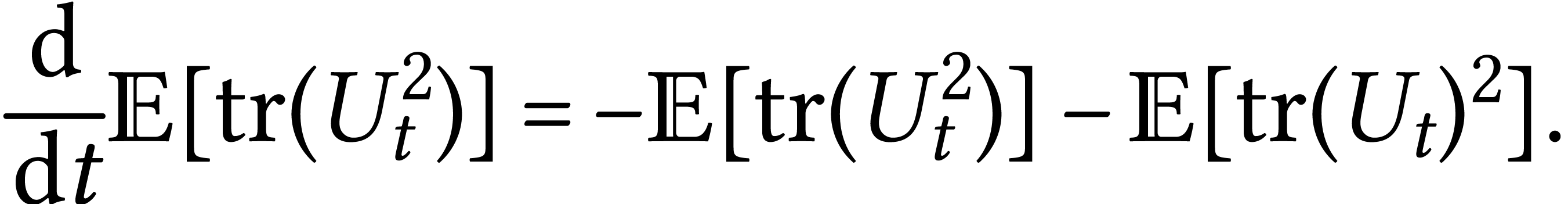 |
(1) |
We are now going to evaluate with similar method 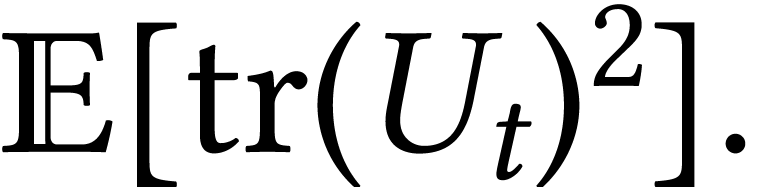
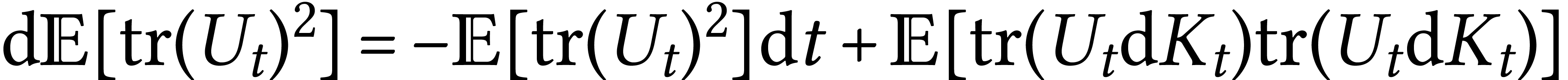
and now use that
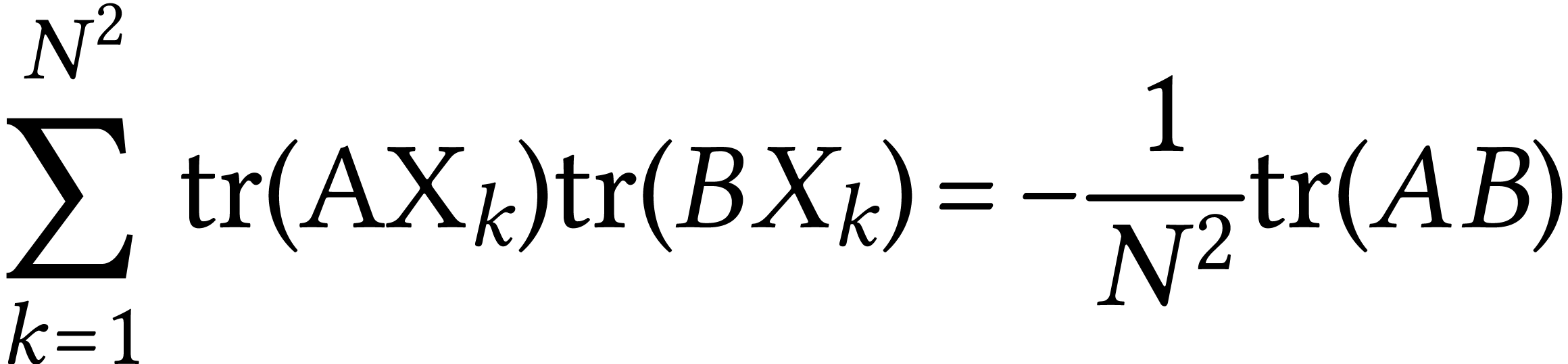
which gives a second equation:
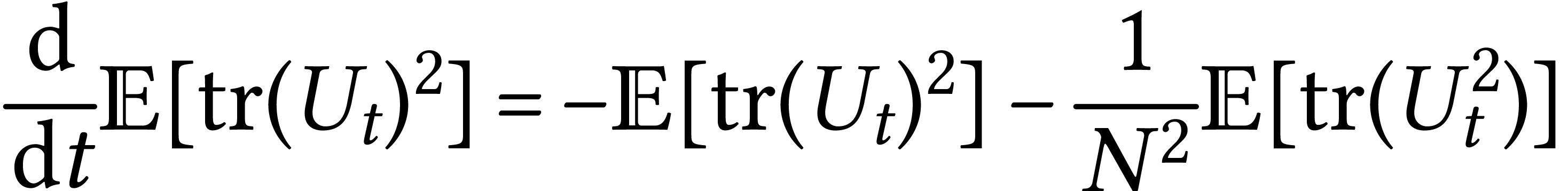 |
(2) |
and (1) (2) form a system of ODEs which can be solved to give:
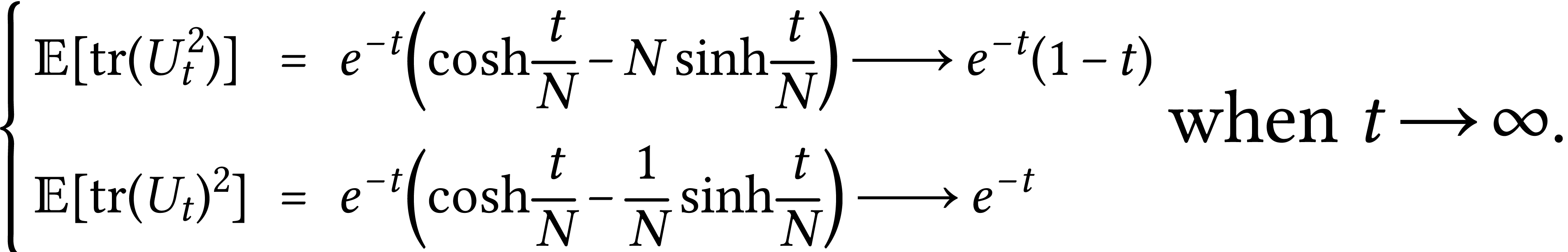
These relations express connections between unitary Brownian motions and the combinatorics of permutations and random walks in the symmetric group.
Take 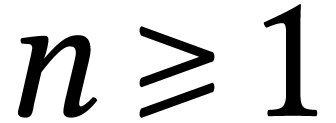 and a permutation
and a permutation 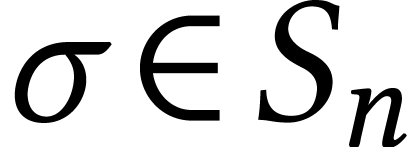 cycle lenghts
cycle lenghts 
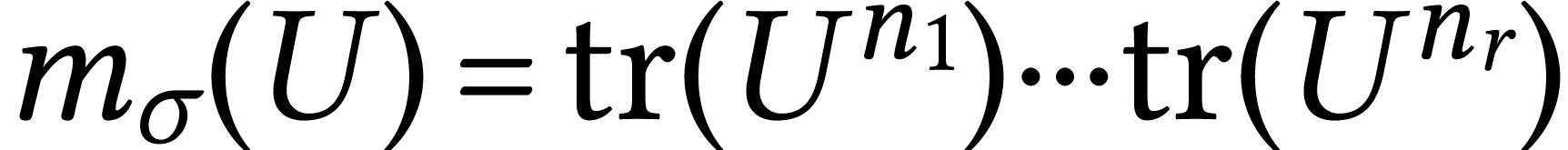
Then I claim that we have
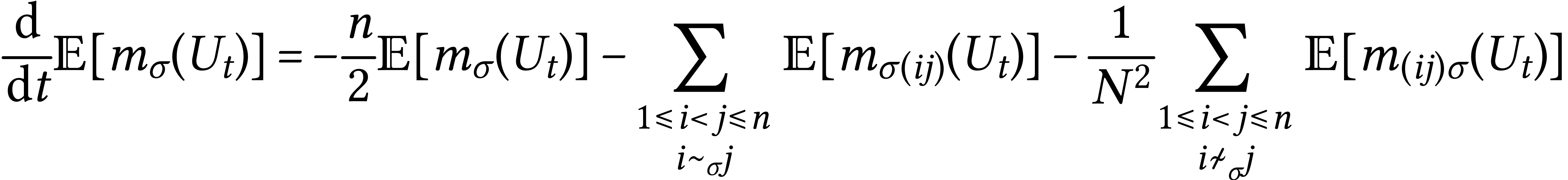
where 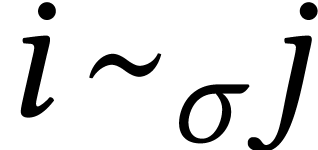 indicate when
indicate when 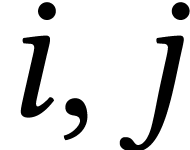 are
in the same cycle of
are
in the same cycle of  .
Therefore, in principle, one can solve this huge family of equations and
taking the
.
Therefore, in principle, one can solve this huge family of equations and
taking the 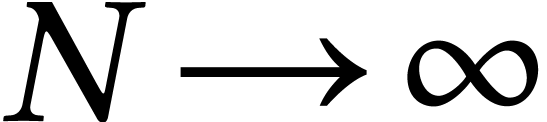 limit one can prove the following
theorem:
limit one can prove the following
theorem:
Theorem
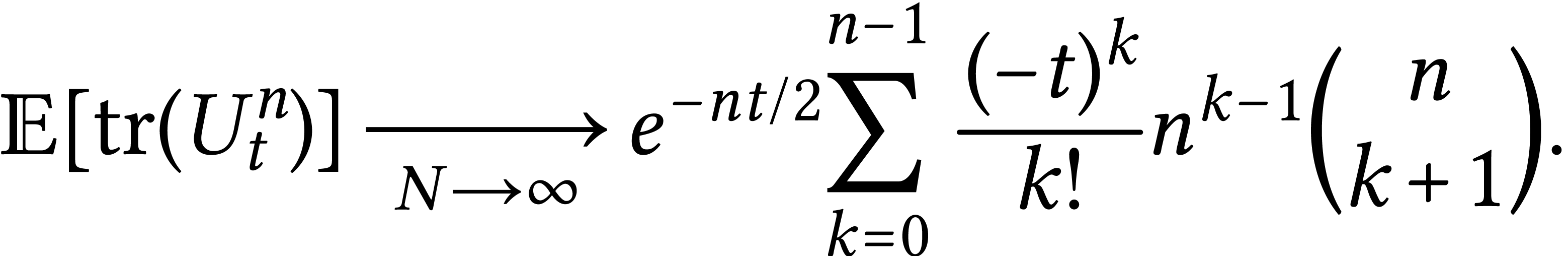
Another theorem says:
Theorem  with group
with group 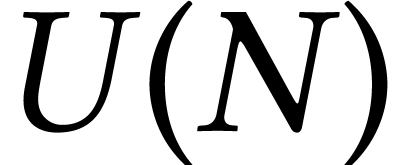 . For any loop
. For any loop 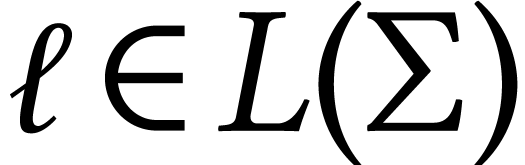

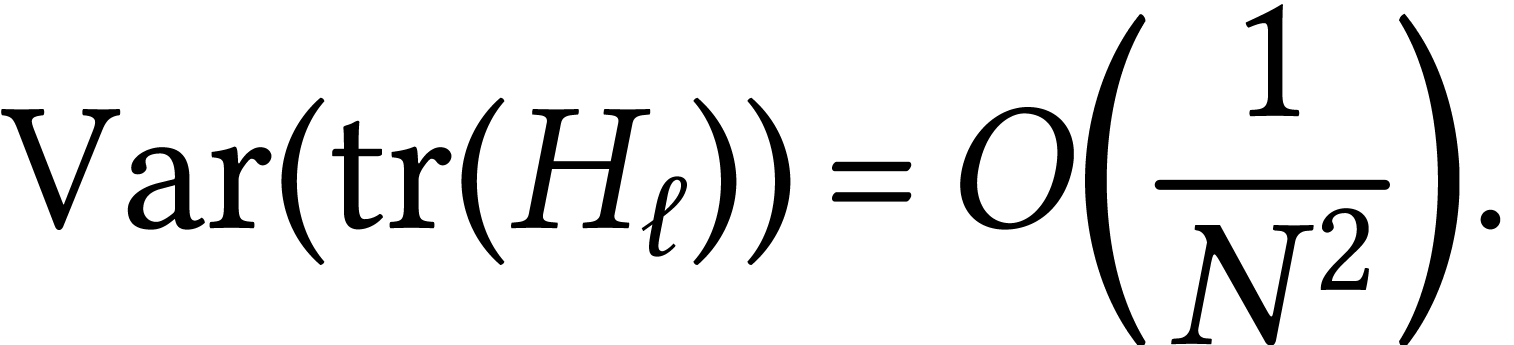
Makeenko–Migdal equation
This last theorem gives a sort of law of large numbers in which it plays a role the function

The MM equations give informations about 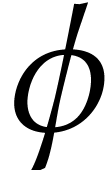 .
Take a loop
.
Take a loop 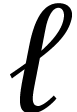 , we want to
compute
, we want to
compute 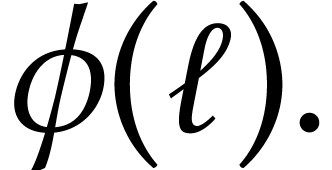 It depends on the combinatorial
structure of the loop and the area of the faces it identifies
It depends on the combinatorial
structure of the loop and the area of the faces it identifies
The MM equations tells us how this number changes when we distort the loop. Look at an intersection
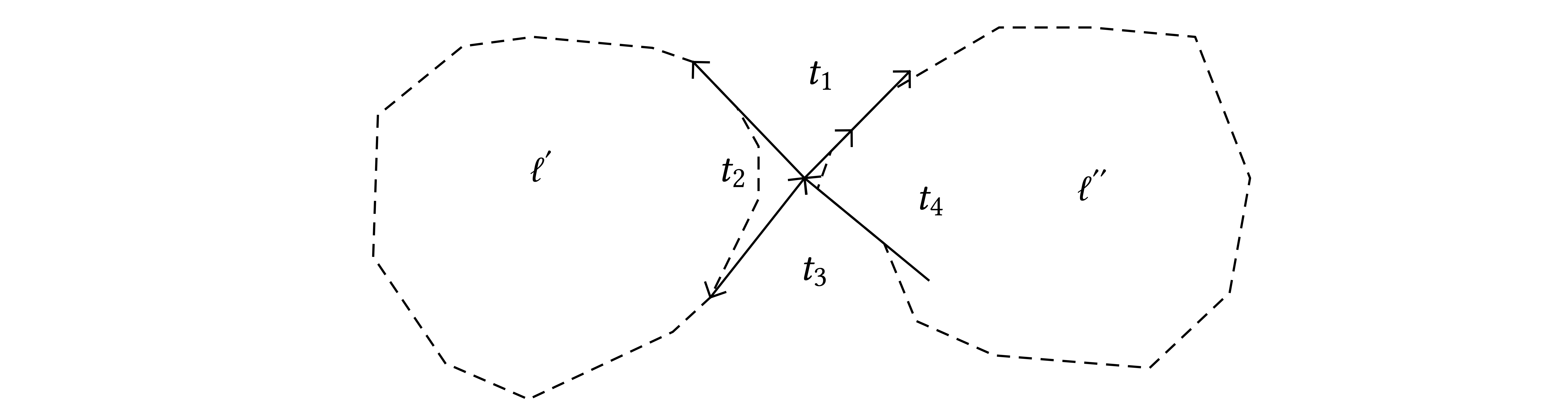
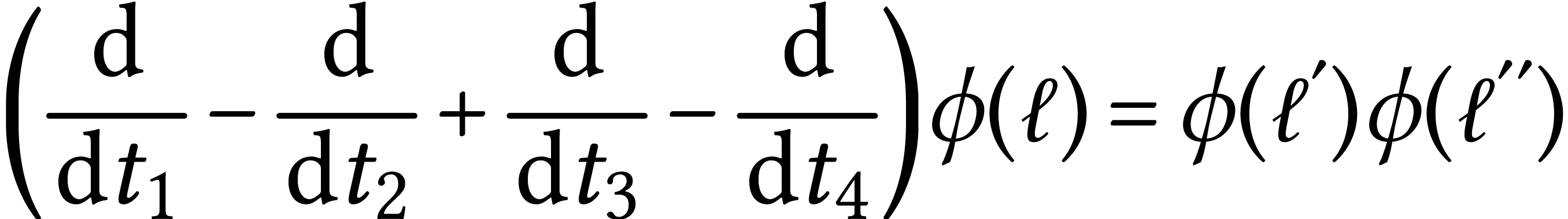
Where  are the loops obtained by removing the
intersection as shown in the picture. The MM equations are known to be
true on the plane and on the sphere and the finite
are the loops obtained by removing the
intersection as shown in the picture. The MM equations are known to be
true on the plane and on the sphere and the finite  version are also known on certain surfaces (which?).
version are also known on certain surfaces (which?).
The value of 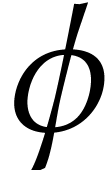 on a simple loop is
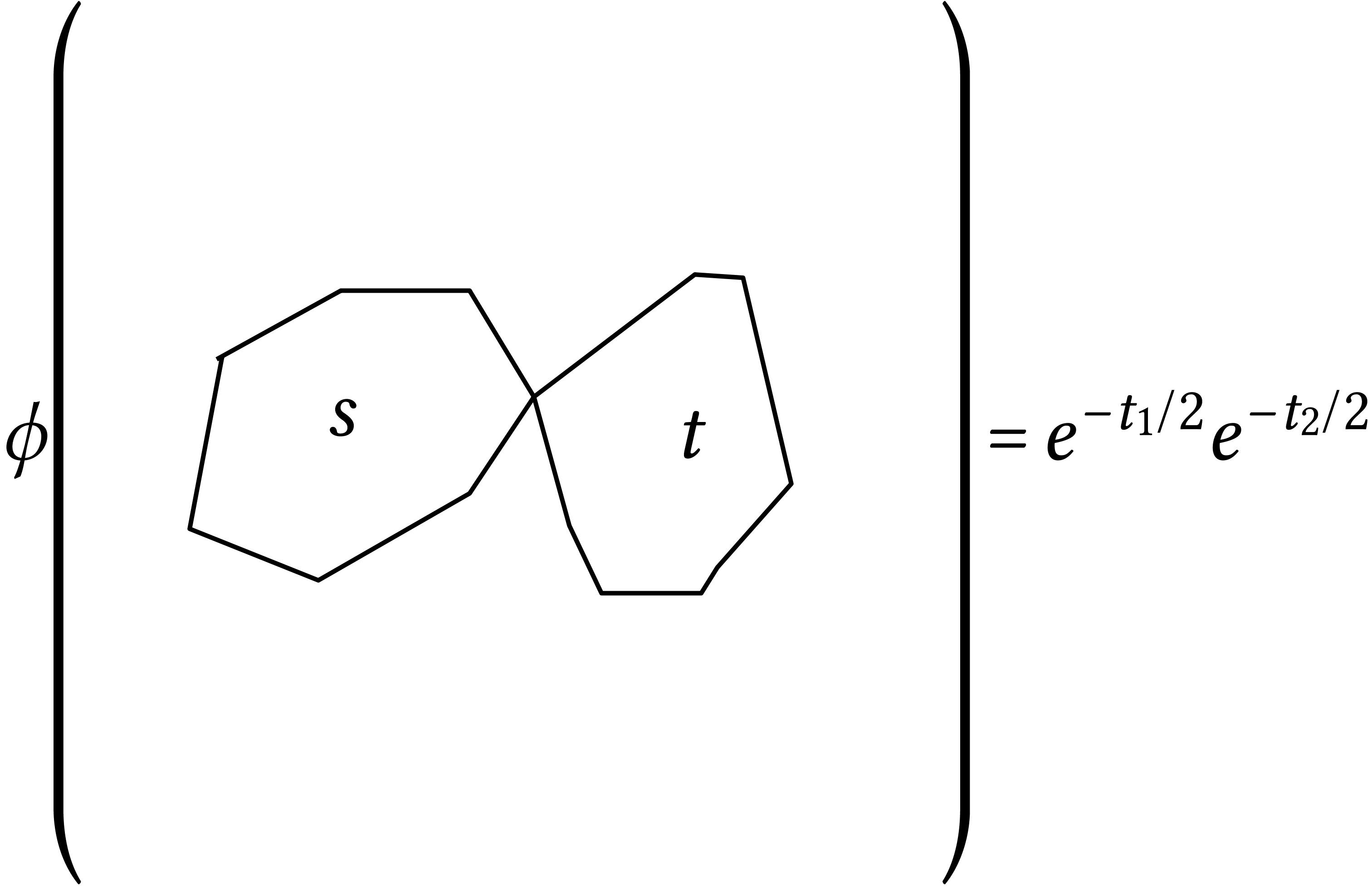
on a simple loop is 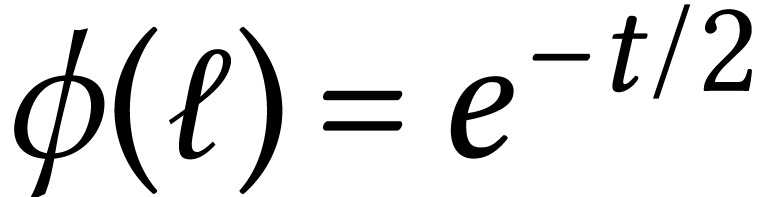 . Loops with one intersection point and
disjoint areas give
. Loops with one intersection point and
disjoint areas give
A loop with on intersection point and one area inside the other (large
area  and small area
and small area 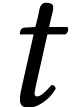 ). Call the value of
). Call the value of
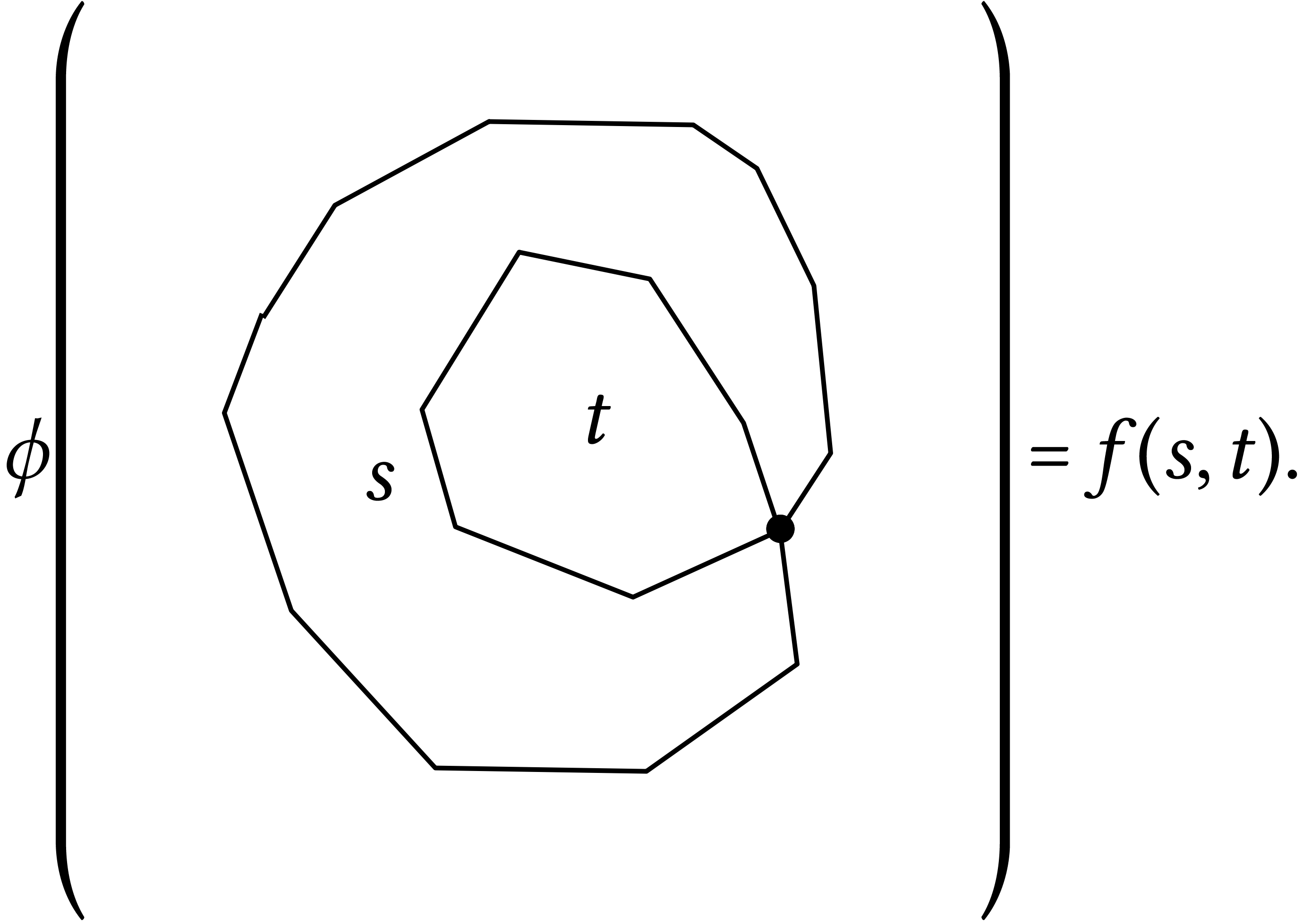
Then
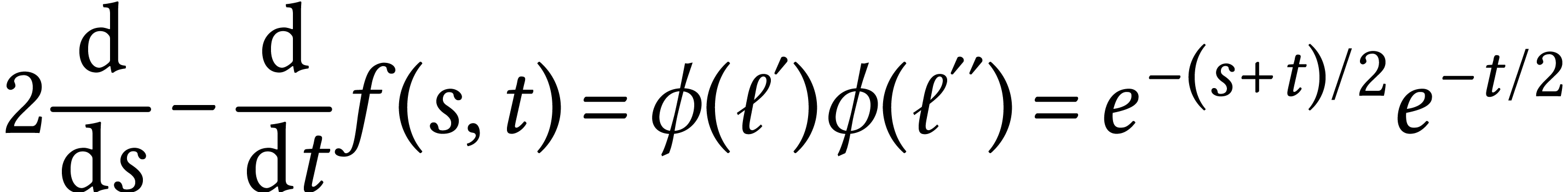
When we change the area of the unbounded face we get
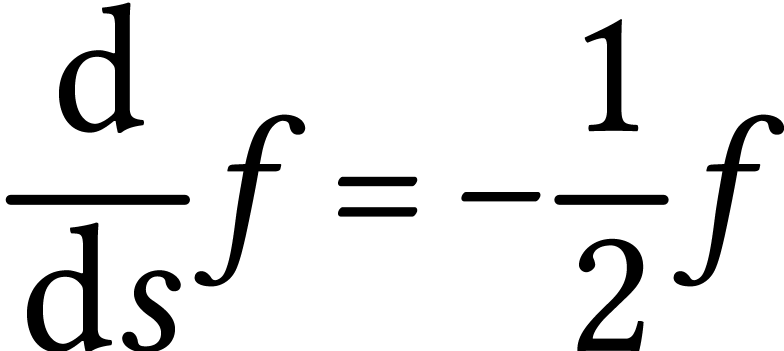
so we can solve and obtain
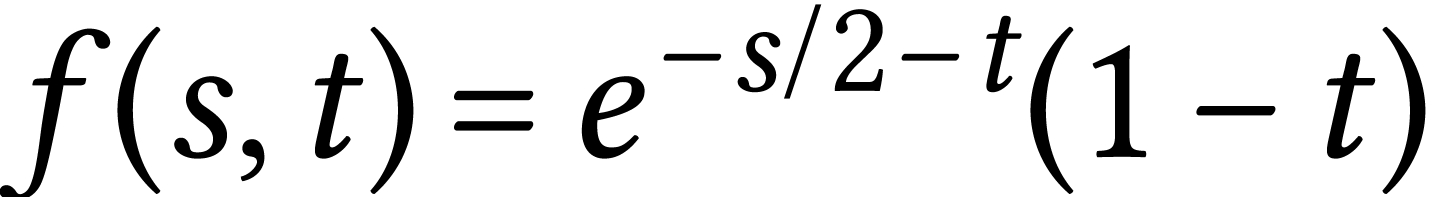
which give the limiting value we found before.