SRQ seminar – October 8th, 2018

Notes from a talk in the SRQ series.

INI Seminar 20181008 Toninelli

Giuliani, Mastropietro, Toninelli (AIHP P&S 2015, J. Stat. 2017, + forthcoming)

Interacting dimer model

A perturbation of an integrable model, solved via renormalization group techniques.

Today: the model, the results and some discussion.

The model

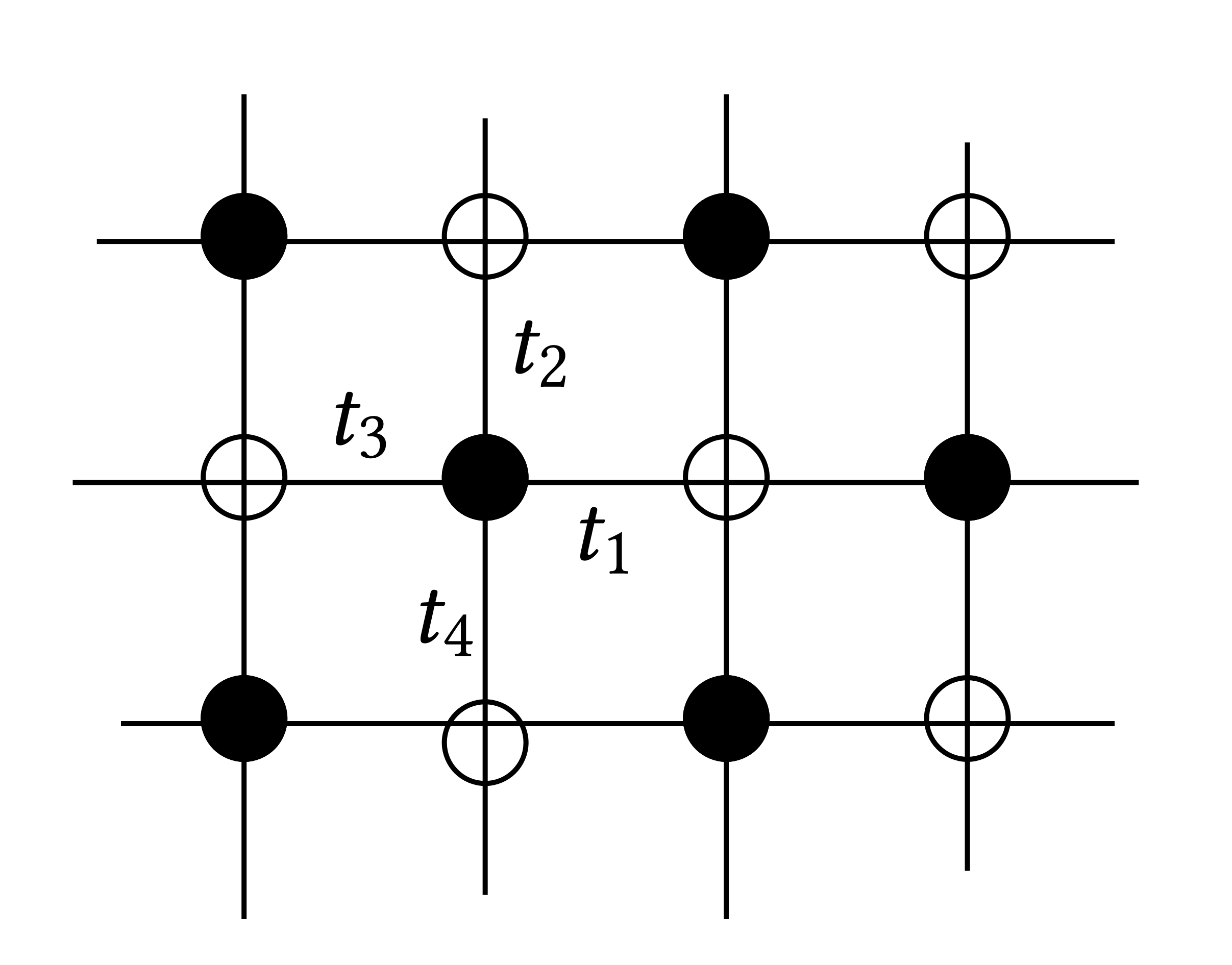
Planar bipartite graph $G = (V, E)$. A dimer configuration (perfect matching). A subset $M \subseteq E$ of edges of $G$ such that every vertex of the graph is contained by exaclty one edge. For us $G \subseteq \mathbb{Z}^2$ with periodic boundary conditions of period $L$. $G$ is a weidghted graph: for every edge there is a weight $(t_e > 0)_{e \in E}$. $4$ weights types for each type of edge (different directions, different initial and final colors)

$\displaystyle \pi_{G, t} (M) \propto \prod_{e \in M} t_e$

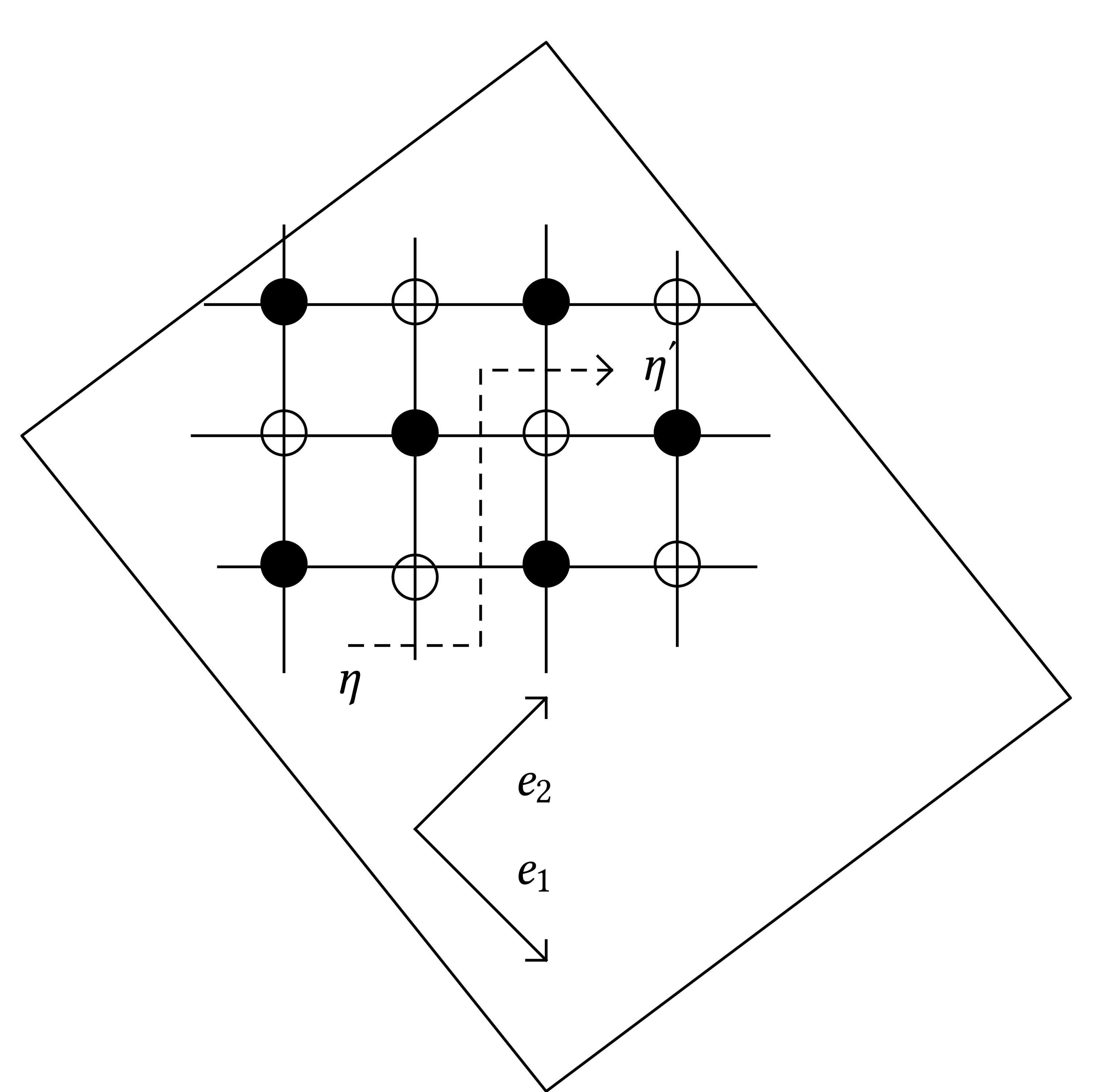
For us $\Lambda =\mathbb{T}_L$ with periodicity $L$ in both directions $e_1, e_2$: ($2 L^2$ vertices)

Height function. For any configuration we can associate an integer valued functions on the faces (vertices of the dual lattice $G^{\ast}$). For any face $\eta \in G^{\ast}$ we let $\eta_M : \text{\{faces\}} \longrightarrow \mathbb{N}$

$\displaystyle h_M (\eta') - h_M (\eta) = \sum_{e : C_{\eta \rightarrow \eta'}} \sigma_e \left( 1_{e \in M} - \frac{1}{4} \right)$

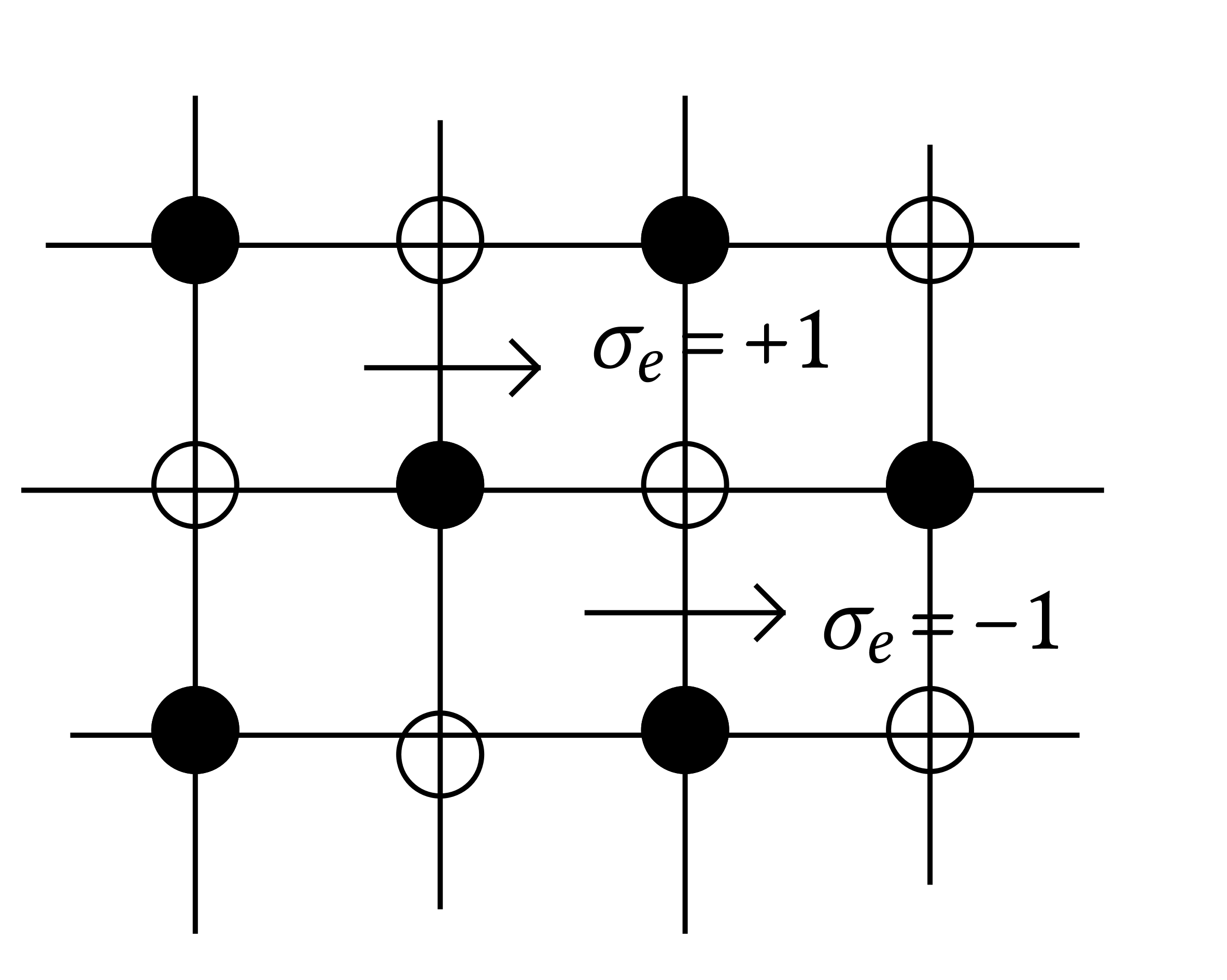
where $\sigma_e \in \{ \pm 1 \}$ is taken according to the rule shown on the right.

This definition of $\eta$ does not depends on the path chosen to go from $\eta$ to $\eta'$ and we choose arbitrarily $h_M (\hat{\eta}) = 0$ for a fixed face $\hat{\eta}$.

Remark 1. on the torus $\mathbb{T}_L$ the height function is not well defined.

A few results on the non-interacting dimer model.

Let $\Pi_{L, \underline{t}}$ the measure on $\mathbb{T}_L$. It has a limit as $L \rightarrow \infty$ $\Pi_{\underline{t}}$ with an explicit and determinantal description (Kasteleyn theory).
The free energe $F (\underline{t}) = \lim_{L \rightarrow \infty} L^{- 1} \log Z_L$ exists and it is explicit.
Comments on the weights $\underline{t}$:
1. one can multiply all the weights by the same factor and this gives the same model. Therefore on can take $t_4 = 1$ w.l.o.g.
2. they are chemical potentials fixing the density of the four type of edges: $\rho_1, \rho_2, \rho_3, \rho_4$. Namely $\rho_j = \Pi_{\underline{t}} (e \in M)$, where $e$ is a fixed edge of type $i$.
3. they fix the global slope of the height function: If we let
  $\displaystyle \Pi_{\underline{t}} [h_M (\eta + e_i) - h_M (\eta)] =: s_i, \qquad i \in \{ 1, 2 \},$
  then $s_i = s_i (\underline{t})$. (Remark: suppose $t_1 = t_3 = t_h$ and $t_2 = t_4 = t_v = 1$, then by symmetry $s_1 = s_2 = 0$.)

Correlations. For the moment take $\underline{t} = (1, 1, 1, 1)$. Then we have a polynomial decay of correlations for the two point function:

$\displaystyle \pi (A ; B) \approx (\operatorname{dist} (A, B))^{- 2} .$

We consider a complex function $K$ of types of edges such that $K (e) = t_1, t_2 (i), t_3 (- 1), t_4 (- i)$ for edges of type $1, 2, 3, 4$ respectively and we let $K_i$ the value of $K (e)$ for an edge of type $i = 1, 2, 3, 4$.

Theorem 2.

$\displaystyle \Pi (\{ e_1, \ldots, e_n \} \in M) = \left[ \prod_{j = 1}^n K (e_j) \right] \det [\mathcal{K}^{- 1} (w_k, b_{\ell})]_{k, \ell = 1, \ldots, n} .$

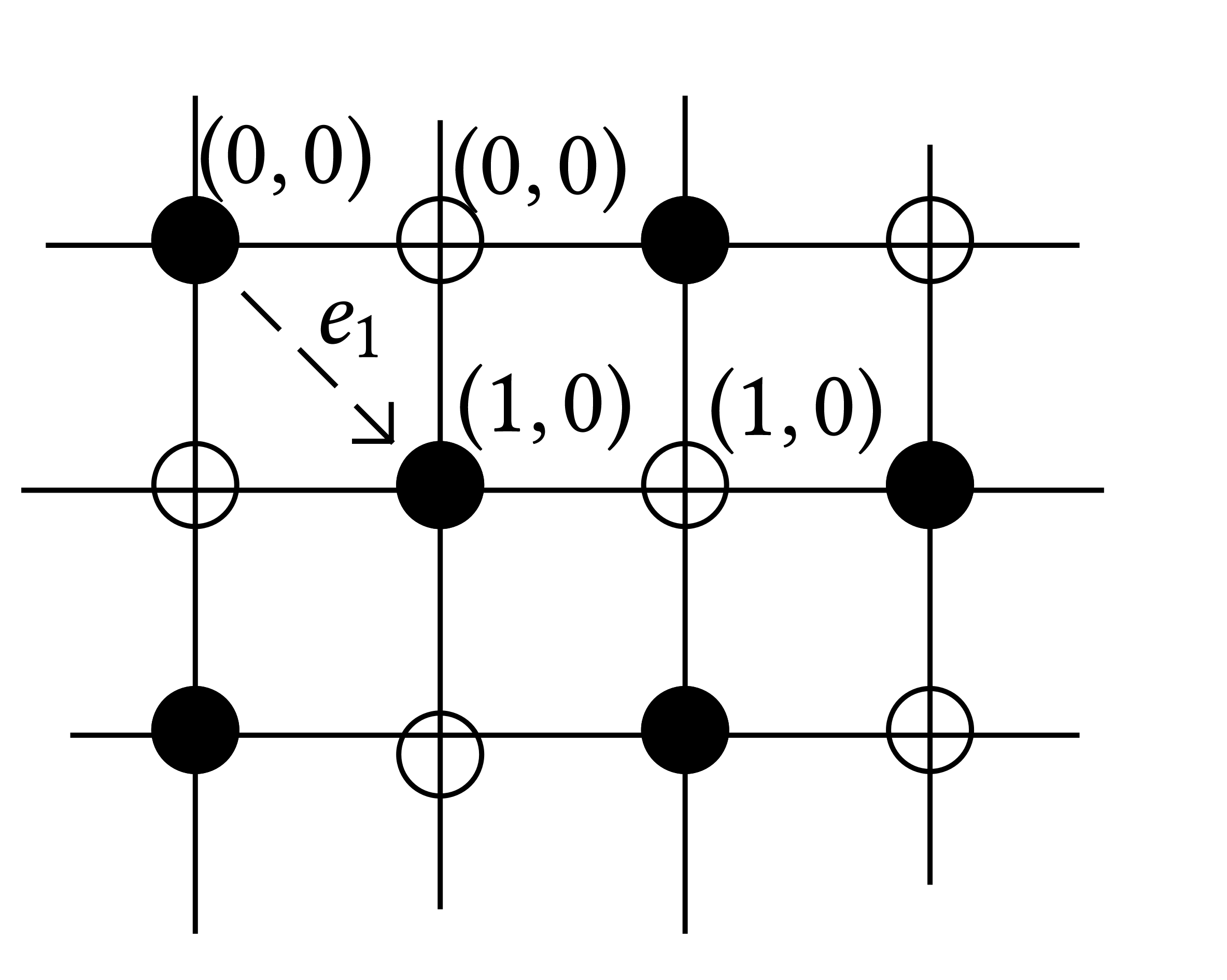
where $w_k, b_k$ are the white and black vertices of the $k$-th edge. Our coordinate system is chosen such that a black vertex of coordinates $(x_1, x_2)$ then the right adjacent vertex is also at coordinates $(x_1, x_2)$.

The matrix $\mathcal{K}^{- 1}$ is given by

$\displaystyle \mathcal{K}^{- 1} (x, y) = \int_{[- \pi, \pi]^2} \frac{\mathrm{d} p}{(2 \pi)^2} \frac{e^{- ip (x - y)}}{\mu (p)}$

with

$\displaystyle \mu (p) = K_1 + K_2 e^{i p_1} + K_3 e^{i (p_1 + p_2)} + K_4 e^{i p_2} .$

Comment: We can consider a matrix $\mathcal{K}$

$\displaystyle \mathcal{K} (b, w) = \left\{ \begin{array}{lll} 0 & & \text{if $w \nsim b$}\\ K_j & & \text{if $b \sim w$ and $(b, w)$ is an edge of type $j = 1, 2, 3, 4$.} \end{array} \right.$

Therefore the result of the theorem can be also written

$\displaystyle \Pi (\{ e_1, \ldots, e_n \} \in M) = \left[ \prod_{j = 1}^n K (b_j, w_j) \right] \det [\mathcal{K}^{- 1} (w_k, b_{\ell})]_{k, \ell = 1, \ldots, n} .$

Exercise 1. if $\underline{t} = (1, 1, 1, 1)$ then $\mu (p)$ vanishes only at $p^+ = (0, 0)$ and $p^- = (\pi, \pi)$ and they are simple zeros (the derivatives are not zero there).

Remark 3. All what we will say later holds under the assumption that $\mu$ has only two simple zeros. In particular when $\underline{t} = (1, 1, 1, 1)$.

$\displaystyle \mathcal{K}^{- 1} (x, y) \cong \frac{1}{2 \pi} \sum_{\omega = \pm 1} \frac{e^{- i p^{\omega} (x - y)}}{\phi_{\omega} (x - y)},$

where

$\displaystyle \phi_{\omega} (x) = \omega (\beta_{\omega} x_1 - \alpha_{\omega} x_2),$

with

$\displaystyle \alpha_{\omega} = \partial_{p_1} \mu (p^{\omega}) = - i - \omega, \quad \beta_{\omega} = \partial_{p_2} \mu (p^{\omega}) = - i + \omega,$

are the derivatives at the poles.

Corollary 4. (edge-edge correlation) Take $e_1$ of type $r_1$ and at $x$ and $e_2$ of type $r_2$ and at $y$, then

$\displaystyle \Pi (e_1 ; e_2) = \Pi (\{ e_1, e_2 \} \in M) - \Pi (\{ e_1 \} \in M) \Pi (\{ e_2 \} \in M) =$

$\displaystyle \propto \det [(\mathcal{K}^{- 1} (w_m, b_n))_{m, n = 1, 2}] - \det [(\mathcal{K}^{- 1} (w_m, b_n))_{m, n = 1}] \det [(\mathcal{K}^{- 1} (w_m, b_n))_{m, n = 2}]$

$\displaystyle = - K (e_1) K (e_2) \mathcal{K}^{- 1} (w_1, b_2) \mathcal{K}^{- 1} (w_2, b_1)$

$\displaystyle \cong_{| x - y | \rightarrow \infty} \frac{1}{2 \pi^2} \operatorname{Re} \left[ \frac{K_{r_1} K_{r_2}}{\phi_+ (x - y)^2} \right] + \frac{(- 1)^{x_1 + x_2 - (y_1 + y_2)}}{4 \pi^2} \cfrac{\overbrace{C_{r_1 r_2}}^{K_{r_1}^{\ast} K_{r_2} + K_{r_1} K^{\ast}_{r_2}}}{| \phi_+ (x - y) |^2} + O \left( \frac{1}{\operatorname{dist} (x, y)^3} \right) .$

Note that $| \phi_+ (x - y) |$ behaves like a distance between in $x, y$ since $\alpha_{\omega}, \beta_{\omega}$ are not colinear in the complext plane.

Height function and the GFF for the non–interacting model

Let $\Delta_{\eta, \eta'} = h (\eta) - h (\eta')$:
$\displaystyle \frac{\operatorname{Var}_{\Pi_{\underline{t}}} (\Delta_{\eta, \eta'})}{\log | \eta - \eta' |} \xrightarrow[| \eta - \eta' | \rightarrow \infty]{} \frac{1}{\pi^2},$
independently of $\underline{t}$ (in the region where $\mu$ has two simple zeros, liquid phase).
The $n$-th cumulant of the differences in height $\Delta_{\eta, \eta'}$ satisfies
$\displaystyle \underbrace{\Pi_{\underline{t}} (\Delta_{\eta, \eta'} ; n)}_{= \partial_{\mu}^n \log \Pi_{\underline{t}} (e^{\mu \Delta_{\eta, \eta'}}) |_{\mu = 0}} =_{| \eta - \eta' | \rightarrow \infty} O (1)$
so the rescaled limit of $\Delta_{\eta, \eta'}$ is Gaussian, namely $\Delta_{\eta, \eta'} / (\operatorname{Var}_{\Pi_{\underline{t}}} (\Delta_{\eta, \eta'}))^{1 / 2} \rightarrow \mathcal{N} (0, 1)$.
Take $\varphi$ a $C^{\infty}$ with compact support on $\mathbb{R}^2$ with average $0$. Consider the rescaled height function $h_{\varepsilon}$ given by
$\displaystyle h_{\varepsilon} (\varphi) = \varepsilon^2 \sum_{\eta} h (\eta) \varphi (\eta \varepsilon),$
then
$\displaystyle h_{\varepsilon} (\varphi) \xrightarrow{d} \mathcal{N} \left( 0, \int_{\mathbb{R}^2 \times \mathbb{R}^2} \mathrm{d} x \mathrm{d} x' \varphi (x) \varphi (x') g (x - x') \right),$
with $g (x) = - \frac{1}{2 \pi^2} \log | \phi_+ (x) | \approx \frac{1}{2 \pi^2} \log \frac{1}{| x |}$. So $h_{\varepsilon}$ converges to a log correlated Gaussian random field.

The interacting dimer model

In the non–interacting the weight of a configuration $w (M) \propto \prod_{e \in M} t_e$. In the interacting case we take $\lambda \in \mathbb{R}$ small and

$\displaystyle w (M) \propto \prod_{e \in M} t_e e^{\lambda W (M)}$

where 

$\displaystyle W (M) = \sum_{x \in \Lambda} f (\tau_x M)$

where $\tau_x M$ is the configuration $M$ translated by $x \in \mathbb{Z}^2$. Examples:

Model 1:

$\displaystyle W (M) = \sum_{\text{face $\eta$ of $\Lambda$ }} \mathbb{I}_{\text{\scriptsize{$\left( \begin{array}{|l|} \eta \end{array} \operatorname{or} \begin{array}{l} \hline \eta\\ \hline \end{array} \right)$}}}$

Model 2:

$\displaystyle f (M) = f \left( \text{\raisebox{-0.5\height}{\includegraphics[width=1.1984126984127cm,height=1.09082710219074cm]{image-1.pdf}}} \right) =\mathbb{I}_{e_1, e_2} +\mathbb{I}_{e_3, e_4}$

Remark: model 2 is equivalent to the $6$–vertex model with weights all $1$ except for one configuration with weight $2 e^{\lambda}$.