[main] [research] [srq]mg|pages

SRQ seminar – October 8th, 2018

Notes from a talk in the SRQ series.

INI Seminar 20181010 Toninelli (revised version 20181012)

Interacting dimer model

\(M\) matchings. \(\Pi_{L, \underline{t}} \propto \prod_{e \in M} t_e\) the non-interacting measure has an infinite volume limit \(\Pi_{\underline{t}}\) which is determinantal. Under the limit measure \(\Pi_{\underline{t}}\) behaves like the massless Gaussian free field. It is true when \(\underline{t} = (1, 1, 1, 1)\) and in an open region of weights.

One can consider \(\varphi \in C_c^{\infty}\) and \(\int \varphi = 0\) and \(\varepsilon^2 \sum_x h (x) \varphi (\varepsilon x) \xRightarrow{d} \mathcal{N} \left( 0, \int \mathrm{d} x \mathrm{d} y \varphi (x) \varphi (y) G (x - y) \right)\) when \(\underline{t} = (1, 1, 1, 1)\).

Propagator of the non-interacting model

\(\displaystyle g (x, y) = \int_{[- \pi, \pi]^2} \frac{\mathrm{d} p}{(2 \pi)^2} \frac{e^{i p (x - y)}}{\mu (p)},\)

with \(\mu (p) = t_1 + i t_2 e^{i p_1} + \cdots\).

\(\displaystyle G (x) = - \frac{1}{2 \pi^2} \log | \phi_+ (x) |\)

where \(\phi_+\) is related to the gradient of \(\mu\) at its two simple zeros \(p^+\) and \(p^-\):

\(\displaystyle \phi_+ (x) = (\beta_+ x_1 - \alpha_+ x_2), \qquad \beta_+ = \partial_{p_2} \mu (p^+), \quad \alpha_+ = \partial_{p_1} \mu (p^+) .\)

and \(\phi_+^{\ast} = - \phi_-\). When \(\)\(\underline{t} = (1, 1, 1, 1)\) we have \(p^+ = (0, 0)\) and \(p^- = (\pi, \pi)\).

Interacting model

\(\displaystyle \Pi_{L, \underline{t}, \lambda} (M) \propto \left( \prod_{e \in M} t_e \right) \exp (\lambda W (M))\)

where \(W (M)\) is a local function of dimer configuration summed over all translations.

Model 1

Model 2

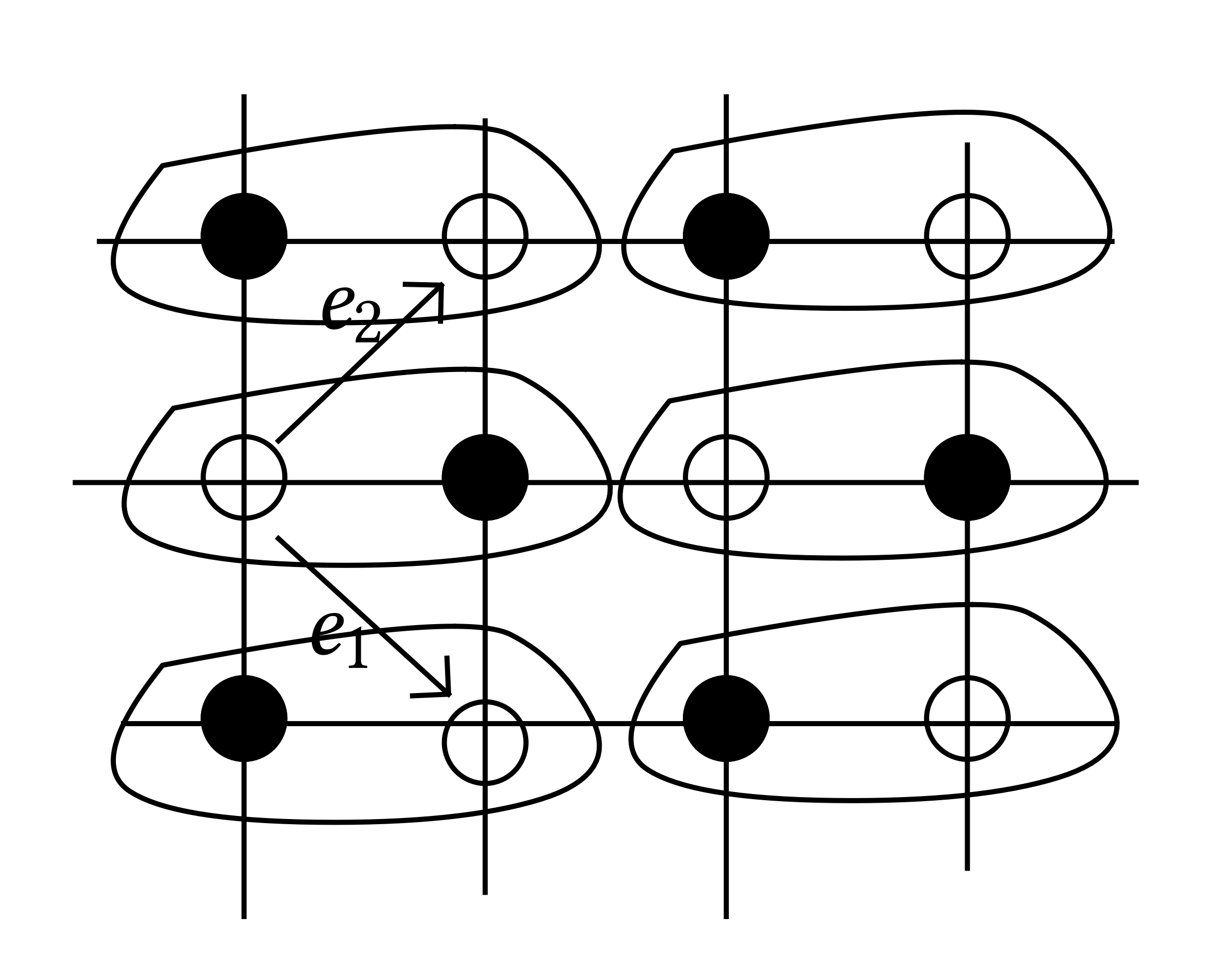
\(\displaystyle W (M) = \sum_{f \in \text{all faces}} \left( \mathbb{I}_{\text{\scriptsize{$\begin{array}{|l|} f \end{array}$}}} +\mathbb{I}_{\text{\scriptsize{$\begin{array}{l} \hline f\\ \hline \end{array}$}}} \right)\)

\(\displaystyle W (M) = \sum_{f \in \text{even faces}} \left( \mathbb{I}_{\text{\scriptsize{$\begin{array}{|l|} f \end{array}$}}} +\mathbb{I}_{\text{\scriptsize{$\begin{array}{l} \hline f\\ \hline \end{array}$}}} \right)\)

(which is linked to the \(6\)-vertex models with \(\Delta = 1 - e^{\lambda}\)) where we say (arbitrarily) that even faces are those having black vertices on the upper left and lower right corners.

We ask \(\lambda \in \mathbb{R}\) being (very) small and \(W\) to be local.

Recall the definition of \(K_r\) depending on the type of edge:

Theorem 1. [AIHP '15] \(\)\(\underline{t} = (1, 1, 1, 1)\) and \(| \lambda | \leqslant \lambda_0\) then

  1. \(\Pi_{L, \underline{t}, \lambda} \rightarrow \Pi_{\lambda}\)

  2. If \(e\) is an edge of type \(r = 1, 2, 3, 4\) and \(b (e) = x\), and \(e'\) is of type \(r'\) and \(b (e') = x'\) then

    \(\displaystyle \Pi_{\lambda} (\mathbb{I}_e ; \mathbb{I}_{e'}) = \frac{A (\lambda)}{2 \pi^2} \operatorname{Re} \left[ \frac{K_{r'} K_r}{\phi_+ (x - x')^2} \right] +\)
    \(\displaystyle + (- 1)^{x_1 + x_2 - (x_1' + x_2')} \frac{C_{r, r'}}{4 \pi^2} B (\lambda) \frac{1}{| \phi_+ (x - x') |^{2 \nu}} + O \left( \frac{1}{| \hspace{1em} \cdots |^{2 + \theta}} \right)\)

    as \(| x - x' | \rightarrow \infty\), where \(\nu = \nu (\lambda)\) and \(A, B\) are analytic functions of \(\lambda\).

  3. The height field converges to a log correlated Gaussian field, for example we have, under \(\Pi_{\lambda}\),

    \(\displaystyle \operatorname{Var} \left[ \frac{h (f') - h (f)}{(\log | f - f' |)^{1 / 2}} \right] \rightarrow \frac{1}{\pi^2} A (\lambda), \qquad \text{as $| f - f' | \rightarrow \infty$},\)

    and in the same limit

    \(\displaystyle \frac{h (f') - h (f)}{(\operatorname{Var} (\cdots))^{1 / 2}} \rightarrow \mathcal{N} (0, 1) .\)

    Note that the oscillating term disappear in the variance.

Remark 2. In Model 1, we worked out \(\nu, A\) which turns out to be

\(\displaystyle \nu (\lambda) = 1 - \frac{4}{\pi} \lambda + O (\lambda^2), \qquad A (\lambda) = \cdots\)

and \(\nu (\lambda)\) depends non–trivially on the weight \(\underline{t}\) but recall that \(\nu (0) = 1\) for any \(\underline{t}\).

Theorem 3. (J.Stat.Mech.) It holds (analog of Haldane's relation for Luttinger liquids)

\(\displaystyle \nu (\lambda) = A (\lambda)\)

for any \(| \lambda | \leqslant \lambda_0\). (Proven for \(\underline{t} = (1, 1, 1, 1)\), but work in progress for more general parameters).

Now we want to show how to represent the correlation functions and partition function as a Grassmann integral.

Kasteleyn theory

\(G \subset \mathbb{Z}^2\) bipartite, admitting perfect matchings like a box \(2 m \times 2 n\).

\(\displaystyle Z_{G, \underline{t}} = | \det \mathcal{K} |\)

where the matrix \(\mathcal{K}\) has row indexed by black and colums indexed by white sites and

\(\displaystyle \mathcal{K} (b, w) = \left\{ \begin{array}{lll} 0 & & \text{if $b \nsim w$}\\ K_r t_r & & \text{if $b \sim w$ and the edge type is $r$} \end{array} \right.\)

On the torus one need to modify the method. One need to define other three matrices \(\mathcal{K}_{\theta_1 {,} \theta_2}\) obtained by multiplying the edges which go out of the torus in direction \(e_1\) by \((- 1)^{\theta_1}\) and in direction \(e_2\) by \((- 1)^{\theta_2 }\), then

\(\displaystyle Z_{G, \underline{t}} = \frac{1}{2} \sum_{\theta_1, \theta_2 = \pm 1} c_{\theta_1, \theta_2} \det \mathcal{K}_{\theta_1, \theta_2}\)

for certain coefficients \(c_{\theta_1, \theta_2}\).

From the formula for the partition function one can derive all the formulas for edge edge correlations.

I will pretend from now on that the partition function is given by a single determinant, namely

\(\displaystyle Z_{L, \underline{t}} = \det \mathcal{K}_{1, 1}\)

because \(\mathcal{K}_{1, 1}\) is invertible. Note that \(\mathcal{K}_{0, 0} = 0\). These matrices are translation invariant so the can be diagonalized in Fourier basis:

\(\displaystyle f_p (w_x) = \frac{1}{L} e^{- i p \cdot x}\)

for \(p \in D = \left\{ (p_1, p_2) : p_i = \frac{2 \pi}{L} \left( n_i + \frac{1}{2} \right), 0 \leqslant n_i \leqslant L - 1 \right\}\) and then

\(\displaystyle \sum_w \mathcal{K} (b, w) f_p (w) = f_p (b) \mu (p) .\)

Therefore from this is easy to deduce that the free energy is

\(\displaystyle F (\underline{t}) = \lim_{L \rightarrow \infty} \frac{1}{L^2} \log Z_{L, \underline{t}} = \int \frac{\mathrm{d} p}{(2 \pi)^2} \log \mu (p)\)

and

\(\displaystyle \mathcal{K}^{- 1} (w_x, b_y) = \frac{1}{L^2} \sum_{p \in D} \frac{e^{- i p \cdot (x - y)}}{\mu (p)} = g (x, y) .\)

We assign Grassmann variables \(\{ \psi^+_x, \psi^-_x \}_{x \in \mathbb{T}_L}\) where \(\psi^+_x\) is on black vertex \(b_x\) and \(\psi^-_x\) on the white vertex \(w_x\). Define the integral of a non–commuting polynomial of the \(\{ \psi^+_x, \psi^-_x \}_{x \in \mathbb{T}_L}\)

\(\displaystyle \int \mathrm{D} \psi \prod_{x \in \Lambda} \psi^-_x \psi^+_x = 1,\)

and the integral change sign when we exchange two variables (so variables cannot appear more than linearly), moreover when any variable is missing the integral is zero.

For example

\(\displaystyle \int \mathrm{D} \psi e^{\psi_1 \psi_2} = \int \mathrm{D} \psi (1 + \psi_1 \psi_2) .\)

A few consequences:

  1. we can rewrite the determinant of a matrix as a Grassmann integral. If \(A\) is an \(n \times n\) matrix, then

    \(\displaystyle \det A = \int \mathrm{D} \psi e^{- \sum_{x, y} A_{x, y} \psi^+_x \psi^-_y} .\)

    Which recall the Gaussian integral

    \(\displaystyle (\det \Sigma)^{1 / 2} = \int \frac{\mathrm{d} x_1 \cdots \mathrm{d} x_n}{(2 \pi)^{n / 2}} e^{- (x, \Sigma^{- 1} x) / 2} .\)

  2. Moreover

    \(\displaystyle A^{- 1} (x, y) = \frac{\int \mathrm{D} \psi e^{- \sum_{x, y} A_{x, y} \psi^+_x \psi^-_y} \psi^-_x \psi^+_y}{\int \mathrm{D} \psi e^{- \sum_{x, y} A_{x, y} \psi^+_x \psi^-_y}}\)

    again similar to the Gaussian formula for the covariance.

  3. Fermionic Wick's rule. Let us denote (with \(A^{- 1} = G\))

    \(\displaystyle \mathcal{E}_G (f) = \frac{\int \mathrm{D} \psi e^{- \sum_{x, y} G^{- 1}_{x, y} \psi^+_x \psi^-_y} f (\psi)}{\int \mathrm{D} \psi e^{- \sum_{x, y} G^{- 1}_{x, y} \psi^+_x \psi^-_y}}\)

    then

    \(\displaystyle \mathcal{E}_G (\psi^-_{x_1} \psi^+_{y_1} \cdots \psi^-_{x_n} \psi^+_{x_n}) = \det [G_n (\underline{x}, \underline{y})]\)

    where we introduce the \(n \times n\) matrix \(G_n (\underline{x}, \underline{y})\) as \(G_n (\underline{x}, \underline{y})_{i, j} = G (x_i, y_j)\) for \(\underline{x} = (x_1, \ldots, x_n)\) and \(\underline{y} = (y_1, \ldots, y_n)\) and \(i, j = 1, \ldots, n\).

For the dimer model we obtain

\(\displaystyle Z = \det \mathcal{K}_{1, 1} = \int \mathrm{D} \psi e^{S (\psi)}, \qquad S (\psi) = - \sum_{x, y} \mathcal{K}_{1, 1} (x, y) \psi^+_x \psi^-_y . \)

The partition function of the interacting model can be also expressed as a fermionic integral. Define

\(\displaystyle e^{W_{\Lambda} (A)} = \sum_M w (M) e^{\sum_{\text{edges}} A_e \mathbb{I}_{e \in M}}\)

where \(A_e \in \mathbb{R}\). This is equivalent to the replacement \(t_e \rightarrow t_e e^{A_e}\) therefore we consider

\(\displaystyle e^{W_{\Lambda} (A)} = \int \mathrm{D} \psi e^{- \sum_{x, y} e^{A_{(b_x, w_y)}} \mathcal{K} (b_x, w_y) \psi^+_x \psi^-_y} = \int \mathrm{D} \psi e^{S_A (\psi)}\)

Proposition 4. When \(W (M) = \sum_{f \in \text{even faces}} \left( \mathbb{I}_{\text{\scriptsize{$\begin{array}{|l|} f \end{array}$}}} +\mathbb{I}_{\text{\scriptsize{$\begin{array}{l} \hline f\\ \hline \end{array}$}}} \right)\) then

\(\displaystyle Z_{\Lambda, \lambda} = \sum_M w (M) e^{\text{\scriptsize{$\lambda \sum_{f \in \text{even faces}} \left( \mathbb{I}_{\text{\scriptsize{$\begin{array}{|l|} f \end{array}$}}} +\mathbb{I}_{\text{\scriptsize{$\begin{array}{l} \hline f\\ \hline \end{array}$}}} \right)$}}} = \int \mathrm{D} \psi e^{S (\psi) + \alpha \sum_{\gamma} \prod_{e \in \gamma} E_e}\)

where \(\gamma = \begin{array}{|l|} f \end{array}, \begin{array}{l} \hline f\\ \hline \end{array}\) and \(E_e = K (e) \psi^+_x \psi^-_x\) if \(e = (b_x, w_y)\) and \(\alpha = e^{\lambda} - 1 \approx \lambda\).

If we are interested in the generating function of the interacting model we replace \(S (\psi) \rightarrow S_A (\psi)\) and \(E_e \rightarrow E_e e^{A_e}\).

\(\displaystyle \)