SRQ seminar – November 21th, 2018

Notes from a talk in the SRQ series.

SRQ 20181121 Levy

The partition function of \(2 d\) YM

(Douglas–Kazakov phase transition)

\(M\) compact oriented surface, possibly with boundary, area is available, everything we talk about behaves well under diffeo which preserve the area.

Invariants up to area preserving diffeos are: genus \(g \geqslant 0\), \(\#\) connected components of \(\partial M\), total area \(T > 0\).

\(G\) compact Lie group, \(\langle \cdot, \cdot \rangle\) on \(\mathfrak{g}\) (the Lie algebra of \(G\)). In our case \(G = U (N)\) and

\(\displaystyle \langle X, Y \rangle = N\operatorname{tr} (X^{\ast} Y) .\)

\(\Gamma\) is a graph \((\mathbb{V}, \mathbb{E}, \mathbb{F})\) embedded in \(M\). Every face is homeomorphic to an open disc. This forces to have the boundary covered by edges and the graph is adapted to the topology of the surface. Here \(\mathbb{E}\) contains both oriented edges and let \(\mathbb{E}^+ \subset \mathbb{E}\) the subset which fixes a particular orientation.

Our configuration space is \(u = (u_e)_{e \in \mathbb{E}^+} \in G^{\mathbb{E}^+}\). This is a discrete version of a gauge field which could interact with particles moving on the graph and carring a state belonging to a space where \(G\) acts.

\(\mu^{\Gamma}\) is a measure on \(G^{\mathbb{E}^+}\). Note that \(G^{\mathbb{E}^+}\) has a canonical probability measure given by taking at random elements from \(G\) for every edge but we put boundary condition on edges on \(\partial M\) using a density (involving the heat kernel) which makes the measure \(\mu^{\Gamma}\) the Yang–Mills measure.

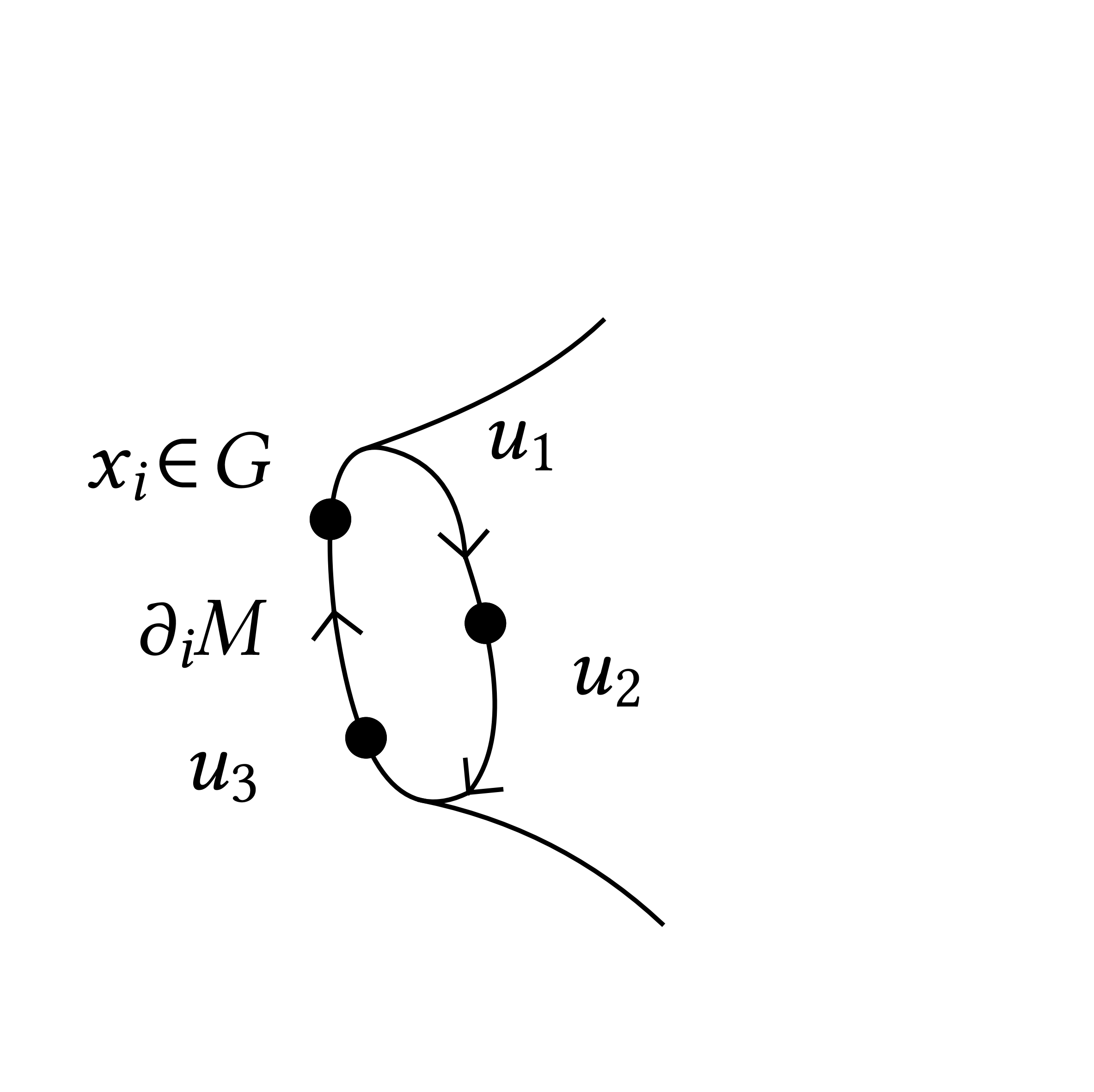
Consider edges on the boundary \(\partial M = \cup_i \partial_i M\). The meaningful boundary conditions are well–defined modulo conjugacy classes. Denote \([x]\) the conjugacy class of \(x \in G\). And now we need to impose that \(u_1 u_2 u_3 \in [x_i]\).

Consider

\(\displaystyle \{ (u_1, u_2, u_3) \in G : u_1 u_2 u_3 \in [x_i] \}\)

now \(G^3\) acts on this space as

\(\displaystyle (v_1, v_2, v_3) \cdot (u_1, u_2, u_3) = (v_1 u_1 v_{1 }^{- 1}, v_2 u_2 v_2^{- 1}, v_3 u_3 v_3^{- 1})\)

and this action is transitive. We want to endow the set above with a \(G^3\)–invariant measure which we denote as

\(\displaystyle \delta_{[x]} (u_1 u_2 u_3) \mathrm{d} u_1 \mathrm{d} u_2 \mathrm{d} u_3\)

and we define as follows. Take \(f : G^3 \rightarrow \mathbb{R}\) and let

\(\displaystyle \int_{G^3} f (u_1, u_2, u_3) \delta_{[x]} (u_1 u_2 u_3) \mathrm{d} u_1 \mathrm{d} u_2 \mathrm{d} u_3 = \int_{G^3} f (w_1, w_2, w_2^{- 1} w_1^{- 1} w^{- 1} x w) \mathrm{d} w \mathrm{d} w_1 \mathrm{d} w_2\)

where \(\mathrm{d} w\) and similar defines the normalized Haar measure on \(G\).

Heat kernel \(K : \mathbb{R}^{\ast}_+ \times G \rightarrow \mathbb{R}^{\ast}_+\): (here \(\Delta_G\) is the Laplace Beltrami operator on \(G\))

\(\displaystyle \left\{ \begin{array}{l} \left( \partial_t - \frac{\Delta_G}{2} \right) K = 0\\ K_t (v) \mathrm{d} v \xRightarrow[t \downarrow 0]{} \delta_1 (\mathrm{d} v) \end{array} \right.\)

Given \(u \in G^{\mathbb{E}^+}\) we define the holonomy \(h_{\partial F} (u)\) of a face \(F \in \mathbb{F}\) \(i \in \{ 1, \ldots, p \}\) and \(h_{\partial_i M} (u)\) the partial holonomy in a connected component of the boundary. They are, as usual, defined up to conjugation.

We define now the lattice \(2 d\) YM measure (Sengupta)

\(\displaystyle \mu^{\Gamma}_{x_1, \ldots, x_p} (\mathrm{d} u) = \frac{1}{Z^{\Gamma}_{x_1, \ldots, x_p}} \cdot \prod_{F \in \mathbb{F}} K_{\text{area} (\partial F)} (h_{\partial F} (u)) \cdot \prod_{i = 1}^p \delta_{[x_i]} (h_{\partial_i M} (u)) \cdot d^{\mathbb{E}^+} u\)

where

\(\displaystyle Z^{\Gamma}_{x_1, \ldots, x_p} := \int_{G^{\mathbb{E}^+}} \prod_{F \in \mathbb{F}} K_{\text{area} (\partial F)} (h_{\partial F} (u)) \cdot \prod_{i = 1}^p \delta_{[x_i]} (h_{\partial_i M} (u)) \cdot d^{\mathbb{E}^+} u.\)

\(Z^{\Gamma}_{x_1, \ldots, x_p}\) does not depend on the graph, it depends only on \(G\), the area and \(x_1, \ldots, x_p\). So

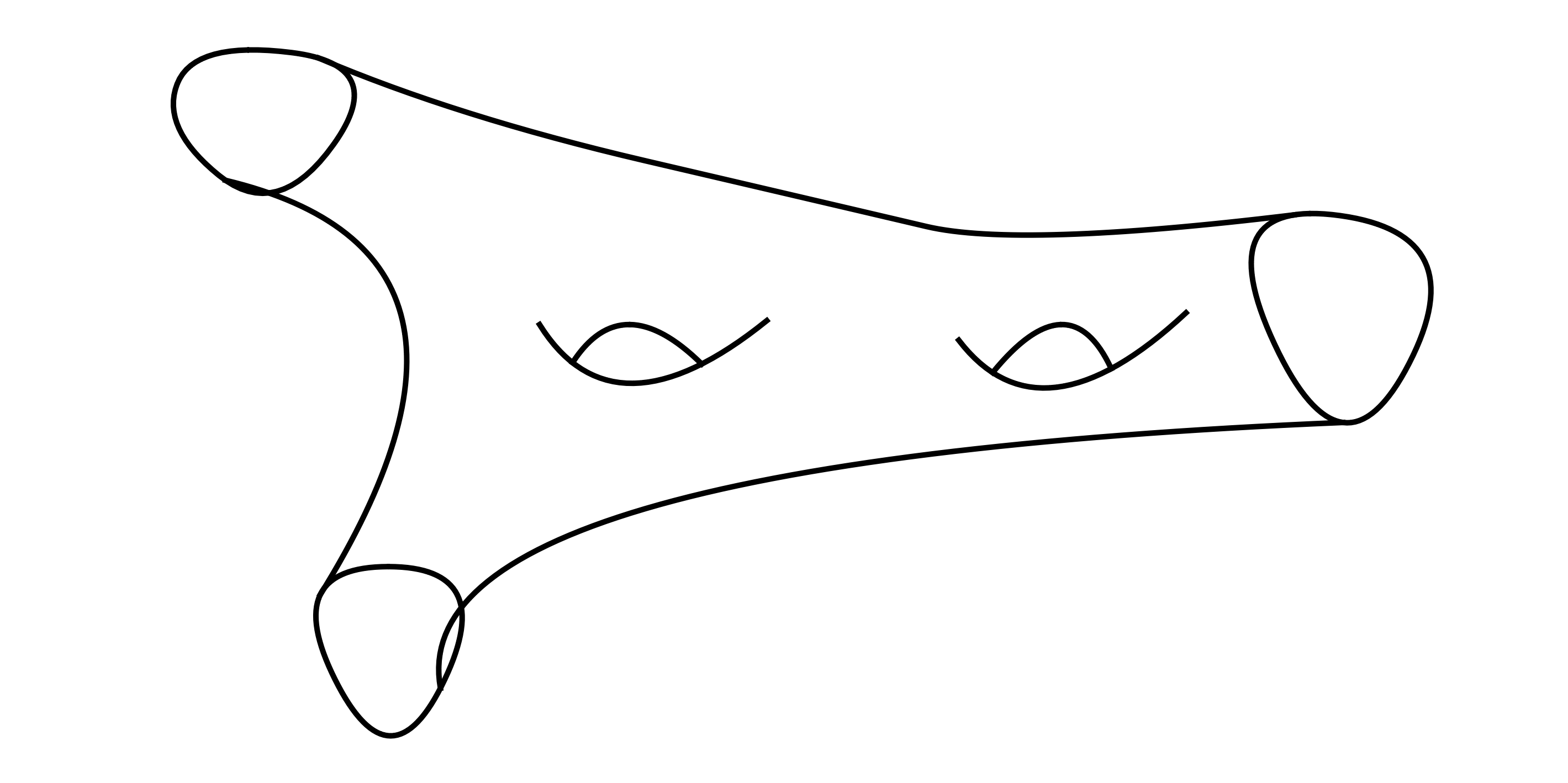
\(\displaystyle Z^{\Gamma}_{x_1, \ldots, x_p} = Z_{T, G, p} (x_1, \ldots, x_p) .\)

How we compute this. Consider a \(g = 2\) surface with \(3\) boundary components and area \(T\), which is homeomorphic to this:

\(\displaystyle \raisebox{-0.5\height}{\includegraphics[width=14.8825429620884cm,height=8.92447199265381cm]{image-1.pdf}}\)

(see Mohar–Bojassen “Curves on surfaces” for the existence of this simple graph). In general we can compute

\(\displaystyle Z_{T, G, p} (x_1, \ldots, x_p) = \int_{G^{2 g + p}} K_T (a_1 b_1 a_1 b_1 \cdots a_g b_g a_g^{- 1} b_g^{- 1} c_1 x_1 c_1^{- 1} \cdots c_p x_p c_p^{- 1}) \mathrm{d} a_1 \cdots \mathrm{d} b_g \mathrm{d} c_1 \cdots \mathrm{d} c_p .\)

In the simplest case it gives:

\(\displaystyle \raisebox{-0.5\height}{\includegraphics[width=14.8825429620884cm,height=8.92447199265381cm]{image-1.pdf}} \qquad Z_{T, 0, 1} = \int_G K_T (c x c^{- 1}) \mathrm{d} c = K_T (x)\)

so the heat kernel is one of these functions. Next,

\(\displaystyle \raisebox{-0.5\height}{\includegraphics[width=14.8825429620884cm,height=8.92447199265381cm]{image-1.pdf}} \qquad Z_{T, 0, 0} = K_T (1)\)

Properties of these functions. (related to surgety of \(2 d\) surfaces)

\(Z_{T, g, p} (x)\) is a symmetric function of \(x_1, \ldots, x_p\) (this corresponds to the fact that diffeos act on the boundary components as the full permutation group)
By gluing two surfaces along a common boundary component we have
\(\displaystyle \int_G Z_{T, g, p} (x_1, \ldots, x_{p - 1}, x_p) Z_{T', g', p'} (x^{- 1}, y_1, \ldots, y_{p' - 1}) \mathrm{d} x\) \(\displaystyle = Z_{T + T', g + g', p + p' - 2} (x_1, \ldots, x_{p - 1}, y_1, \ldots, y_{p' - 1}) .\)
which expresses a “Markovian” property of the YM measure.
\(\displaystyle \int_G Z_{T, g, p} (x_1, \ldots, x_{p - 2}, x, x^{- 1}) \mathrm{d} x = Z_{T, g + 1, p - 2} (x_1, \ldots, x_{p - 2}) .\)

In particular we can reconstruct all these functions from very few building blocks, namely: a cap

\(\displaystyle \raisebox{-0.5\height}{\includegraphics[width=14.8825429620884cm,height=8.92447199265381cm]{image-1.pdf}} \qquad Z_{T, 0, 1} (x)\)

and pants:

\(\displaystyle \raisebox{-0.5\height}{\includegraphics[width=14.8825429620884cm,height=8.92447199265381cm]{image-1.pdf}} \qquad Z_{T, 0, 3} (x_1, x_2, x_3)\)

Let's go back to

\(\displaystyle Z_{T, g, p} (x_1, \ldots, x_p) = \int_{G^{2 g + p}} K_T (a_1 b_1 a_1 b_1 \cdots a_g b_g a_g^{- 1} b_g^{- 1} c_1 x_1 c_1^{- 1} \cdots c_p x_p c_p^{- 1}) \mathrm{d} a_1 \cdots \mathrm{d} b_g \mathrm{d} c_1 \cdots \mathrm{d} c_p .\)

Consider \(G = U (N)\) and \(M = S^2\) with \(\langle X, Y \rangle = N^2 \operatorname{Tr} (X^{\ast}, Y)\).

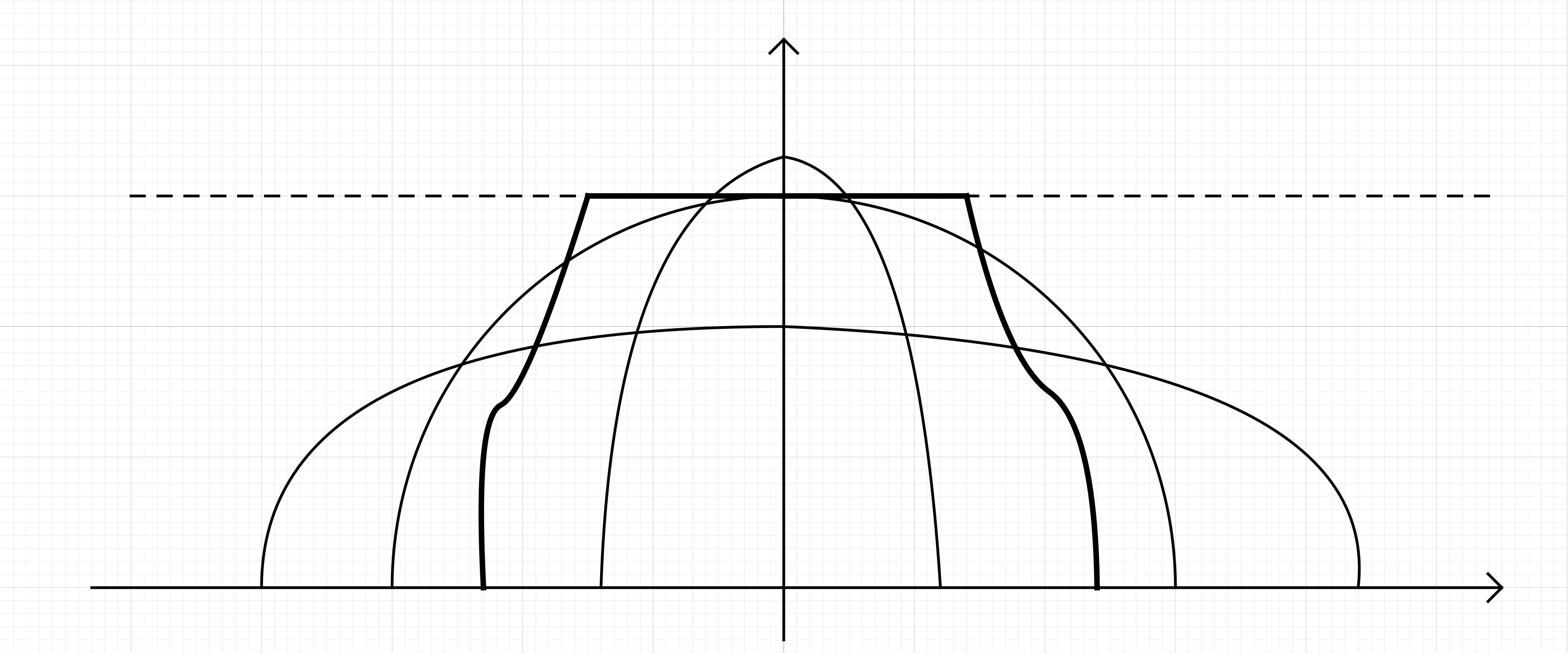
Theorem. The limit below exists:

\(\displaystyle F (T) = \lim_{N \rightarrow \infty} \frac{1}{N^2} \log K_T (I_N)\)

and \(F\) is \(C^2\) on \(\mathbb{R}^{\ast}_+\), is \(C^{\infty}\) on \(\mathbb{R}^{\ast}_+ \backslash \{ \pi^2 \}\) and

\(\displaystyle F''' (\pi^2 - 0) = - \frac{1}{\pi^6}, \qquad F''' (\pi^2 + 0) = - \frac{3}{\pi^6} .\)

The results is due to Douglas–Kazakov and the first proof is due to Liechty–Wang (2015) and a subsequent proof is given by Levy–Maïda (2016).

A proof goes via Fourier expansion of the heat kernel: (on any compact Lie group)

\(\displaystyle K_T (x) = \sum_{\alpha \in \hat{G}} e^{- \frac{c_2 (\alpha) T}{2}} \underbrace{\chi_{\alpha} (1)}_{\text{dim} (\alpha)} \chi_{\alpha} (x)\)

\(\hat{G}\) is the set of irreducible representations of \(G\) and \(\Delta \chi_{\alpha} = - c_2 (\alpha) \chi_{\alpha}\). Using this Fourier expression and elementary properties of characters \(\chi_{\alpha}\) of the representation we can also compute that

\(\displaystyle Z_{T, g, p} (x_1, \ldots, x_p) = \sum_{\alpha \in \hat{G}} e^{- \frac{c_2 (\alpha) T}{2}} \chi_{\alpha} (1)^{2 - 2 g} \frac{\chi_{\alpha} (x_1)}{\chi_{\alpha} (1)} \cdots \frac{\chi_{\alpha} (x_p)}{\chi_{\alpha} (1)} .\)

and

\(\displaystyle K_T (1) = \sum_{\alpha \in \hat{G}} e^{- \frac{c_2 (\alpha) T}{2}} \chi_{\alpha} (1)^2 .\)

When \(G = U (N)\) we have

\(\displaystyle \widehat{U (N)} =\mathbb{Z}_{\downarrow}^N = \{ (\ell_1 > \cdots > \ell_N) \in \mathbb{Z}^N \} .\)

Taking \(\ell = (\ell_1 > \cdots > \ell_N)\) we have \(c_2 (\ell) \cong \| \ell \|^2\) and

\(\displaystyle \chi_{\ell} (I_N) = \frac{V (\ell_1, \ldots, \ell_N)}{V (1, \ldots, N)} = \frac{\prod_{i < j} (\ell_i - \ell_j)}{\prod_{i < j} (i - j)}\)

where \(V\) is the Vandermonde determinant.

\(\displaystyle K_T (1) = \sum_{\ell \in \mathbb{Z}^N_{\downarrow}} e^{- \frac{\| \ell \|^2 T}{2}} V (\ell)^2\)

and

\(\displaystyle \widehat{\mu_{\ell}} = \frac{1}{N} \sum_{i = 1}^N \delta_{\ell_i / N}\)

and

\(\displaystyle e^{- \frac{\| \ell \|^2 T}{2}} V (\ell)^2 \approx \exp \left[ - N^2 \left( \int_{x \neq y} (- \log | x - y |) \mathrm{d} \hat{\mu}_{\ell} (x) \mathrm{d} \hat{\mu}_{\ell} (y) + \frac{T}{2} \int x^2 \mathrm{d} \hat{\mu}_{\ell} (x) \right) \right]\)

so we have a confining potential and electrostatic repulsion. The minimizing configurations are exactly those which give rise to the semicircle distribution. Due to the excluded volume constraint coming from the structure of \(\mathbb{Z}^N_{\downarrow}\) we are looking to minimizers within the class of measures with density \(\leqslant 1\). For small time the absolut minimizer satisfies naturally this constraint. But for \(T = \pi^2\) the constraint is saturated and for \(T > \pi^2\)

\(\displaystyle \)